Progress

This module introduces all the concepts that we use to prove that system trajectories progress towards their goals. These concepts are described in terms of labeled directed graphs.

Labeled Graphs

A labeled graph is defined by: (1) a set of vertices, (2) a set of labels and (3) a set of edges. An edge is defined by its originating vertex, its label and its terminating vertex. We use the notation \( v \stackrel{a}{\rightarrow} w \) to represent an edge from \(v\) to \(w\) with label \(a\). There can be multiple outgoing edges with the same label from a vertex. For example, \(v \stackrel{a}{\rightarrow} w \) and \(v \stackrel{a}{\rightarrow} u \) can both exist where \(w\) and \(u\) are different. There can be multiple edges between a pair of vertices. For example, \(v \stackrel{a}{\rightarrow} w \) and \(v \stackrel{b}{\rightarrow} w \) can both exist.

Restriction: We restrict attention to graphs in which for every vertex \(v\) and every label \(a\) there exists at least one outgoing edge from \(v\) with label \(a\). Note that an edge can be from a vertex back to itself.

Example 1

Fig2 — Fig.1 - Example 1 of a Labeled Graph

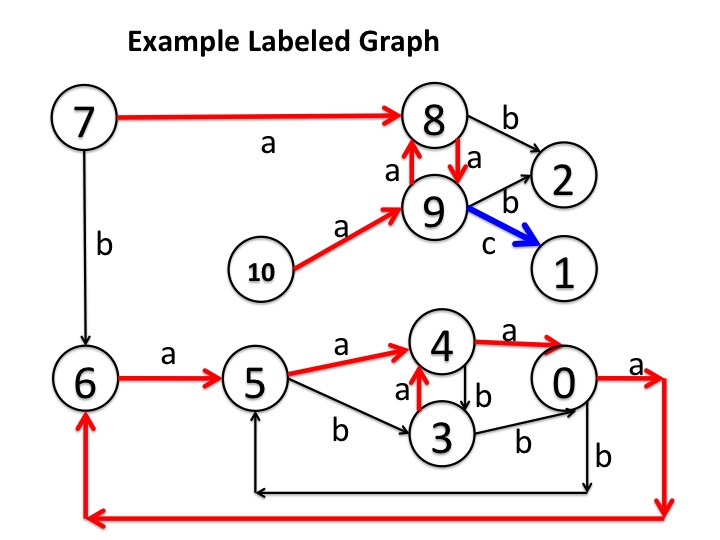
In this example, the edges are labeled \(a\), \(b\), \(c\), and each vertex has exactly one outgoing edge with each label. So as not to crowd the diagram, edges from a vertex to itself are not shown. For example, vertex \(7\) has an edge labeled \(c\) back to itself; vertex \(10\) has edges labeled \(b\) and \(c\) back to itself, and vertex \(2\) has edges labeled \(a\), \(b\) and \(c\) back to itself.

Paths in Labeled Graphs

A path is defined by a sequence of edges where the terminating vertex of an edge is the originating vertex of the next edge in the sequence. For example, a path \(p\) is denoted by:
\( p_{0} \stackrel{a_{0}}{\rightarrow} p_{1} \stackrel{a_{1}}{\rightarrow} p_{2} \stackrel{a_{2}}{\rightarrow} \ldots p_{i} \stackrel{a_{i}}{\rightarrow} p_{i+1} \stackrel{a_{i+1}}{\rightarrow} \ldots \)
where \(p_{i}\) is the \(i\)-th vertex visited on the path, and the sequence of edges in the path are \(p_{i} \stackrel{a_{i}}{\rightarrow} p_{i+1}\) for \(i \geq 0\), and \(p_{0}\) is the initial vertex of the path.

Example of a Path: \( 7 \stackrel{a}{\rightarrow} 8 \stackrel{b}{\rightarrow} 2 \stackrel{c}{\rightarrow} 2 \stackrel{a}{\rightarrow} 2 \stackrel{b}{\rightarrow} 2 \stackrel{c }{\rightarrow} 2\ldots \)

Paths that Traverse a Label Infinitely Often

A path \(p\) traverses label \(L\) infinitely often exactly when at every point in \(p\) there is a later point at which \(p\) traverses an edge labeled \(L\). So, the gaps between successive traversals of \(L\) are finite.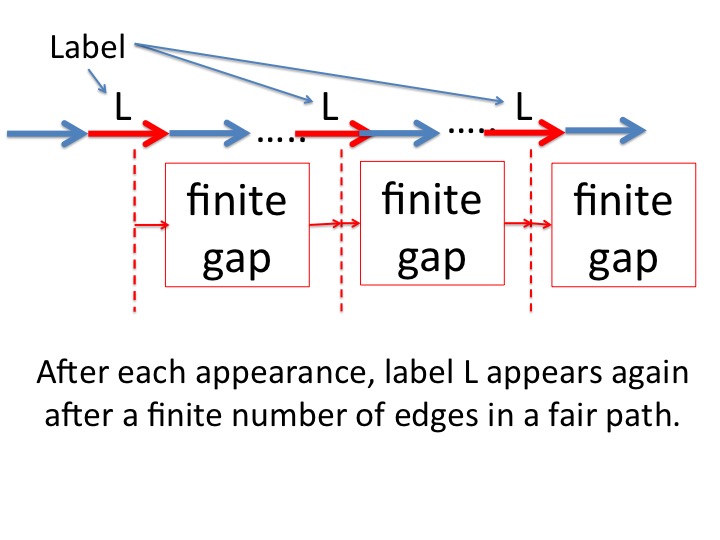

Fig0 — Path that traverses label L infinitely often

Let \(l_{j}\) be the label of the edge from vertex \(p_{j}\) to vertex \(p_{j+1}\). Path \(p\) traverses label \(L\) infinitely often exactly when:

\(\forall j: \; \exists k > j: \; l_{k} = L \)

Example of a path that traverses a label infinitely often

Let \(p\) be the path that repeatedly cycles through vertices \(3\) and \(4\) traversing an edge with label \(a\) and then an edge with label \(b\).

\( 3 \stackrel{a}{\rightarrow} 4 \stackrel{b}{\rightarrow} 3 \stackrel{a}{\rightarrow} 4 \stackrel{b}{\rightarrow} 3 \stackrel{a}{\rightarrow} 4 \stackrel{b}{\rightarrow} 3 \ldots \)

\(p\) traverses edges with label \(a\) infinitely often, and it also traverses edges with label \(b\) infinitely often.

Fair Labels

Now we consider labeled graphs in which a subset of labels are designated as fair labels. We define a fair path in such a graph as follows: A path \(p\) is a fair path exactly when \(p\) traverses every fair label infinitely often.

A label that is not fair may appear an arbitrary number of times in fair paths: it may appear a finite number of times or it may appear infinitely often. Labels that are not fair represent events, such as errors, over which designers have no control. An error may never occur, or it may occur a few times, or it may occur infinitely often.

Examples of Fair Paths

Consider the case, shown in Figure 1, where the fair labels are \(a\) and \(b\). An examples of a fair path is: \( 3 \stackrel{a}{\rightarrow} 4 \stackrel{b}{\rightarrow} 3 \stackrel{a}{\rightarrow} 4 \stackrel{b}{\rightarrow} 3 \stackrel{a}{\rightarrow} 4 \stackrel{b}{\rightarrow} 3 \ldots \)

An example of a path that is not fair

\( 8 \stackrel{b}{\rightarrow} 8 \stackrel{a}{\rightarrow} 9 \stackrel{a}{\rightarrow} 8 \stackrel{a}{\rightarrow} 9 \stackrel{a}{\rightarrow} 8 \stackrel{a}{\rightarrow} 9 \stackrel{a}{\rightarrow} 8 \ldots \)

This path traverses an edge labeled \(b\) once and thereafter traverses only edges labeled \(a\). This path is not fair because it only traverses infinitely-often label \(b\) only a finite number of times.

Example 2

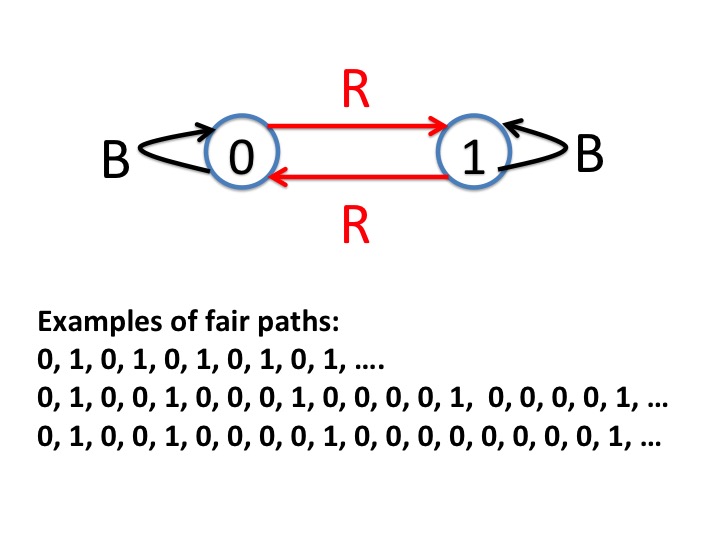
This example illustrates that fairness does not imply equality. This graph has fair edges labeled R (red) and B (black). The first path shown in the diagram has equal number of both labels: \( 0 \stackrel{R}{\rightarrow} 1 \stackrel{B}{\rightarrow} 0 \stackrel{R}{\rightarrow} 1 \stackrel{B}{\rightarrow} 0 \stackrel{R}{\rightarrow} \ldots \)

This path is fair because all labels appear infinitely often. The second path in the diagram has label \(1\) appearing after \(n\) successive appearances of label \(2\) where \(n\) grows linearly. The ratio of the number of \(1\) labels to the number of \(0\) labels is vanishingly small as the path length increases. Nevertheless, the second path is also fair because labels \(0\) and \(1\) appear infinitely often.

In the third path in the diagram, label \(1\) appears after \(n\) successive appearances of label \(2\) where \(n\) grows exponentially. Nevertheless, this path is also fair.

Leads-To, \(\leadsto\)

\(\leadsto\), read as "leads to," is a binary relation on vertex sets. \(P \leadsto Q\) holds exactly when every fair path that visits a vertex in \(P\) later visits a vertex in \(Q\).

\( P \leadsto Q \; \equiv \; \forall \; \textrm{fair} \; p: \; p_{i} \in P \; \Rightarrow \; \exists j > i: p_{j} \in Q \)

An example of \(P \leadsto Q\)

In Fig. 1: \( \{8, 9\} \leadsto \{1, 2\} \)
A fair path that enters any vertex in \(\{8, 9\}\) cannot remain in \(\{8, 9\}\) for ever because the path will traverse infinitely-often label \(b\) which takes the path out of \(\{8, 9\}\). Transitions out of \(\{8, 9\}\) are to \(\{1, 2\}\).

An example of \(\neg (P \leadsto Q)\)

In Fig. 1: \( \neg (\{7\} \leadsto \{1, 2\}) \)
There is a fair path from \(7\) through \(6\) that never visits \(\{1, 2\}\). So, not all fair paths from \(7\) visit \(\{1, 2\}\).

Example 3

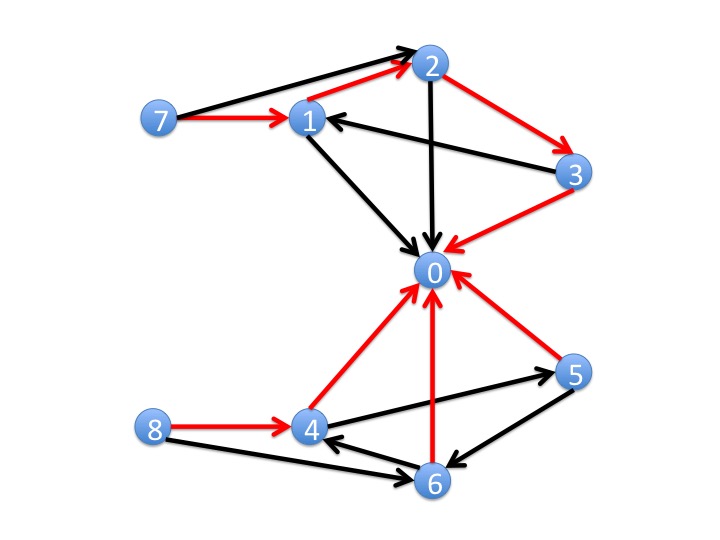
This graph, Figure 3, has two labels, red and black, shown by the color of the edges. Both labels are fair.

Is \(\{1\} \leadsto \{0\}\) true?

No.
\(1 \leadsto 0\) holds only if all fair paths from vertex \(1\) visit vertex \(0\). The following is a fair path starting at vertex \(1\) which never visits vertex \(0\):

\( 1 \stackrel{R}{\rightarrow} 2 \stackrel{R}{\rightarrow} 3 \stackrel{B}{\rightarrow} 1 \stackrel{R}{\rightarrow} 2 \stackrel{R}{\rightarrow} 3 \stackrel{B}{\rightarrow} 1 \stackrel{R}{\rightarrow} \ldots \)

where the labels R and B stand for red and black, respectively. This path is fair because all fair labels appear infinitely often in the path.

Is \(\{4\} \leadsto \{0\}\) true?

Yes.
Every path from vertex \(4\) that traverses a red edge visits vertex \(0\). Every fair path must traverse red edges infinitely often.

More examples of \(P \leadsto Q\)

\( \{8\} \leadsto \{4, 6\} \)

\( \{8\} \leadsto \{0\} \)

\( \{4, 5, 6\} \leadsto \{0\} \)

\( \neg (\{7\} \leadsto \{0\}) \)

Eventually, \(E\)

We define a function \(E\) from vertex sets to vertex sets as follows. A vertex \(v\) is in \(E(Q)\) exactly when all fair paths from \(v\) visit \(Q\).

\( v \in E(Q) \; \equiv \; v \leadsto Q \)

Read \(E(Q)\) as "eventually Q."

You can use either \(E\) or \(\leadsto\) because:

\( (P \leadsto Q) \quad \equiv \quad (P \subseteq E(Q)) \)

So, \(E(Q)\) is the weakest set \(P\) such that \(P \leadsto Q\).

In this course, we use \(\leadsto\) more often than \(E\). You should, however, be able to rewrite formulae that use \(\leadsto\) into formulae that use \(E\), and be equally facile with both concepts.

An example of Eventually: E(P)

is: \( E({1, 2}) = \{1, 2, 8, 9, 10\} \) because all paths that start at vertices in \(\{1, 2, 8, 9, 10\}\) and that traverse labels \(a\) and \(b\) infinitely often, visit vertices \(1\) and \(2\).

Relationship between Labeled and Unlabeled Graphs

The concepts we use to reason about safety are defined in terms of unlabeled graphs but they apply to labeled graphs as well. For example \(v \rightarrow w\) holds exactly when there is an edge from vertex \(v\) to vertex \(w\), regardless of the label on the edge.

Summary

This course is structured around the concepts \(\rightarrow\) and \(\leadsto\). This module and the previous module on safety define the fundamental concepts that we use to reason about systems.

When we use a concept, such as \(stable\) that is defined in terms of the basic concepts, we will give its definition again. We will also show the equivalence of formulae that use \(\rightarrow\) and \(\leadsto\) in those that use \(N\), \(A\), and \(E\).

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology