Resource Management: Drinking Philosophers

This module describes algorithms for "The Distributed Drinking Philosophers Problem," by which distributed agents share indivisible resources, such as exclusive access to files.

Key Ideas

1. This module describes algorithms by which distributed agents share indivisible resources, such as exclusive access to files, in a fair way.
2. The module shows how to use a total ordering of priorities to share resources fairly. The dining philosophers algorithm, given in an earlier module, uses a partial ordering.
3. We show how time --- readings from local clocks of agents --- is used to obtain priorities that are totally ordered.

The description of the algorithm in this module is not as detailed as that given for dining philosophers. You can define a formal specification and carry out a detailed proof for this algorithm in almost exactly the same was as for dining philosophers.

The Problem

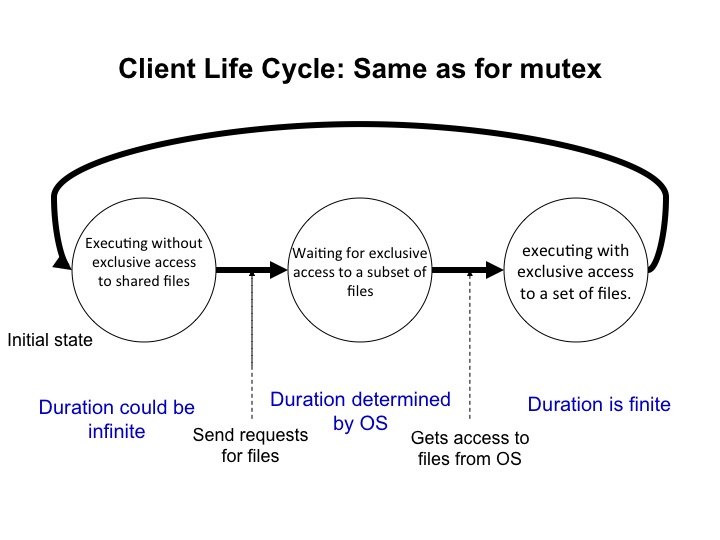
A set of agents shares a set of indivisible resources. Exclusive access to a file is an example of an indivisible resource.

The lifecycle of an agent is the same as in Dining Philosophers: (1) executing outside the critical section, (2) waiting to enter a critical section, and (3) executing in the critical section. The problem is identical to Dining Philosophers except for the transition to the critical section.

An agent executes outside the critical section without holding any resources. An agent may execute outside critical sections for ever, or it may start waiting to enter a critical section. When an agent starts waiting to enter a critical section it waits to get exclusive access to a nonempty subset of the resources. It continues waiting until it gets all the resources for which it waits. While it waits it does not change the subset of resources for which it waits. The agent continues to hold these resources when it executes in the critical section. An agent remains in a critical section for only a finite number of steps and then starts executing outside the critical section at which point it no longer needs resources.

For example, an agent needs exclusive access to a set of files for it to execute in its next critical section, and it waits until it is given this access. While it is in the critical section it continues to have exclusive access to these files. When it is executing outside the critical section it does not need access to these files. Each time an agent starts to wait it may wait for a different set of files.

The ideas in this module can be used to manage agents that require read or write access to files. Multiple agents can have read access to a file concurrently. While an agent has write access to a file no other agent can have access to the file. A homework problem deals with read/write access.

Drinking Philosophers

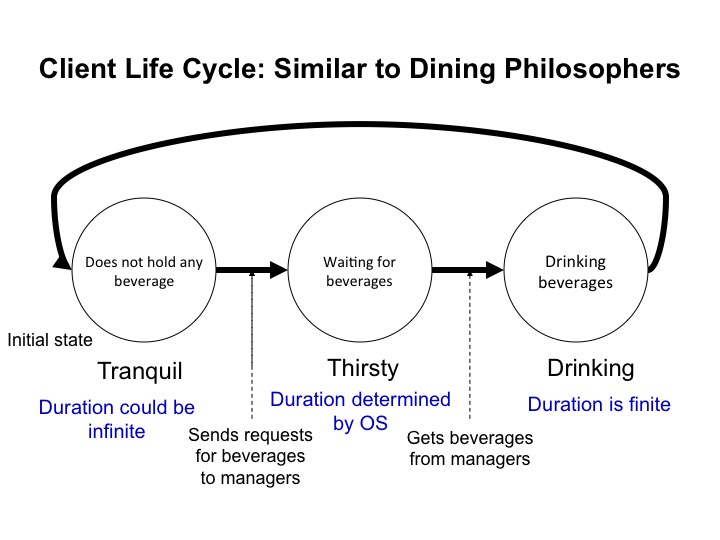
The drinking philosophers name is another example of an attempt at CS humor. A philosopher is in one of three states: tranquil, thirsty or drinking. A philosopher may remain tranquil for ever, or it may become thirsty for one or more beverages. It remains thirsty until it gets all the beverages for which it waits. Only when a thirsty philosopher gets all the beverages for which it waits does it start drinking. It continues to drinking all these beverages until it becomes tranquil again. Philosophers drink for only finite time.

A philosopher that enters the tranquil state remains in that state for at least a constant \(\gamma\) amount of time. So, a philosopher can't go from drinking to thirsty instantaneously or in an arbitrarily small amount of time.

A beverage can be held by at most one philosopher. Imagine there's only one bottle of each beverage in the system, and philosophers send bottles to each other. One philosopher can drink vodka and cola while another philosopher drinks gin and tonic. However, one agent cannot drink vodka and cola while another drinks vodka and orange juice.

An Algorithm

There are many algorithms for this problem; here we discuss one. Each beverage is an indivisible unique token. A token is exchanged between agents and a manager of the token. We assume that each token has its own manager --- this assumption is merely for convenience of exposition.

Messages

1. request: An agent sends a request for a beverage to a manager. A request is a pair \(agent\_id, request\_priority\), the id of the requestor and the priority of the request.
2. beverage: A manager sends a beverage to a requesting agent, and agents send beverages back to managers. A beverage is uniquely identified by its name.
3. demand: A manager sends a demand to an agent for the beverage that the manager manages and that the agent holds.

Agent Actions

1. When an agent becomes thirsty it sends requests to managers for all the beverages that it needs to drink.
2. If a thirsty agent gets a demand to return a beverage to a manager then the agent returns the beverage and sends another request for the beverage. The priority of this new request is the same as the priority of this agent's last request.
3. If a thirsty agent gets all the beverages that it needs to drink then it starts drinking.
4. When an agent finishes drinking it returns all the beverages that it holds to the managers of the beverages.

Manager Actions

A manager has local variable \((hr, hp)\), which is the id of the agent to which the manager has most recently sent the beverage, and the priority of the request made by that agent. \(hr\) is an acronym for handling requestor, and \(hp\) is an acronym for handling priority. If the manager holds the beverage then this variable is empty (\(Null\)).

A manager also maintains a priority queue of pending requests ordered by priority.

The actions of a manager are as follows.

1. If a manager gets a request \((r, p)\) while it holds a beverage then it sends the beverage to the requestor \(r\), and sets \(hr, hp = r, p\).
2. If a manager gets a request \((r, p)\) while it does not hold the beverage and \(hp > p\) then the manager inserts the request \((r, p)\) into the priority queue of pending requests.
3. If a manager gets a request \((r, p)\) while it does not hold the beverage and \(hp < p\) then:
   1. the manager sends a demand to \(hr\) to return the beverage, if the manager has not already sent that demand, and
   2. the manager inserts the request \((r, p)\) into its priority queue of pending requests.
4. If a manager gets a beverage and it has no pending requests then the manager holds the beverage and sets the handling requestor and priority to empty.
5. If a manager gets a beverage and it has pending requests then let \((r, p)\) be the request at the head of the priority queue (i.e. the request with the highest priority). It sends the beverage to requestor \(r\), removes \((r, p)\) from the queue of pending requests, and sets \(hr, hp = r, p\).

Example

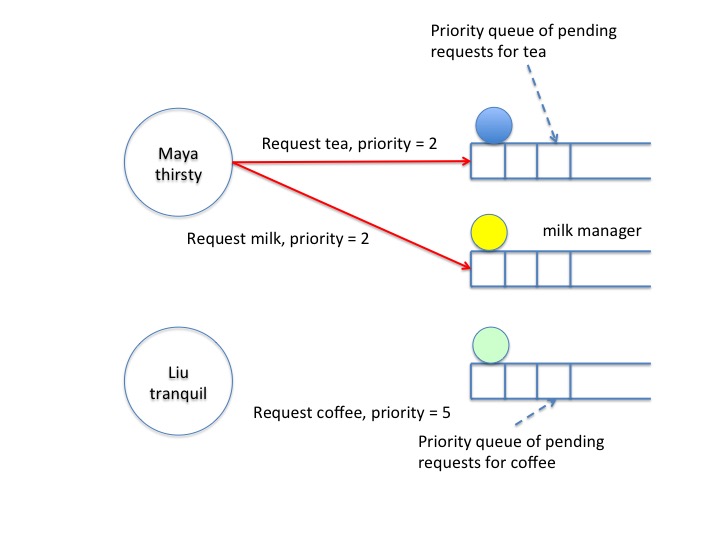
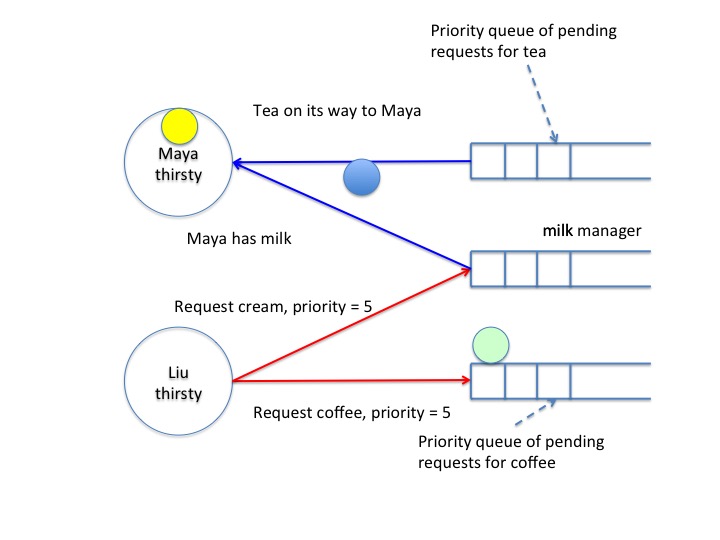
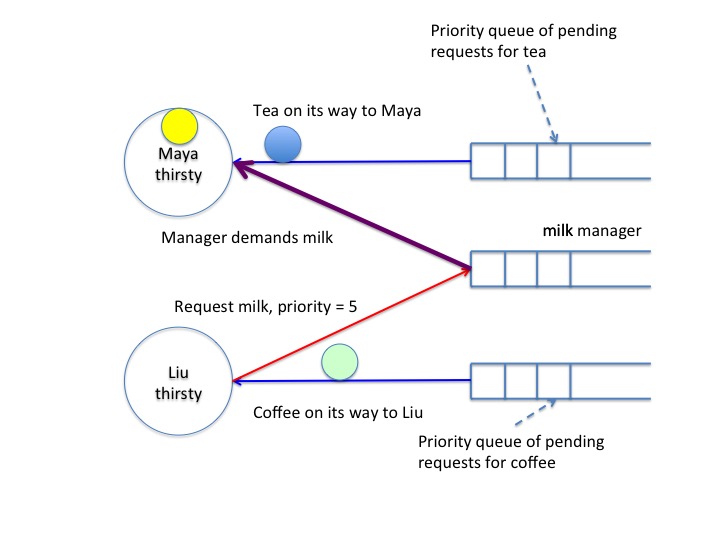
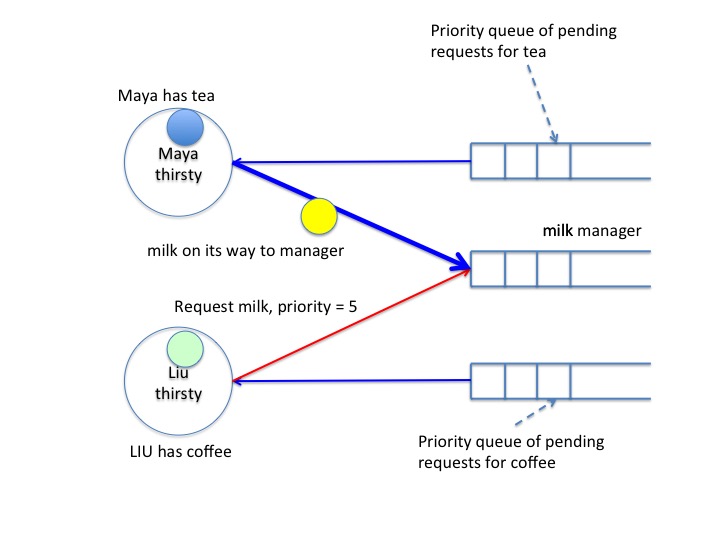
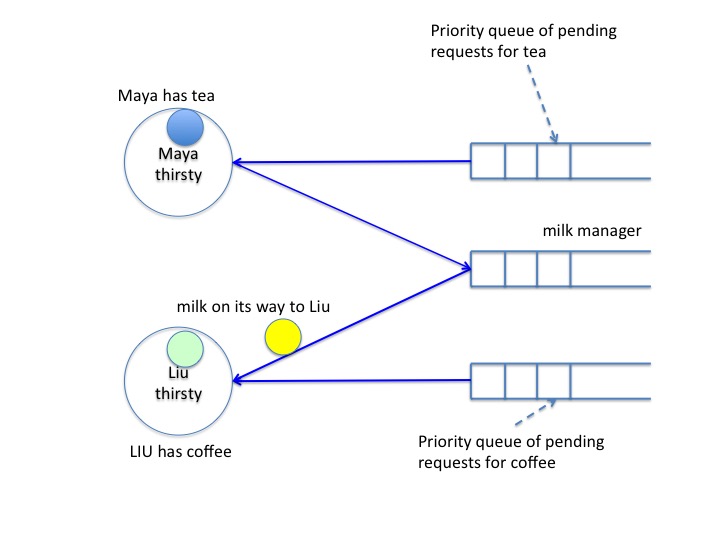
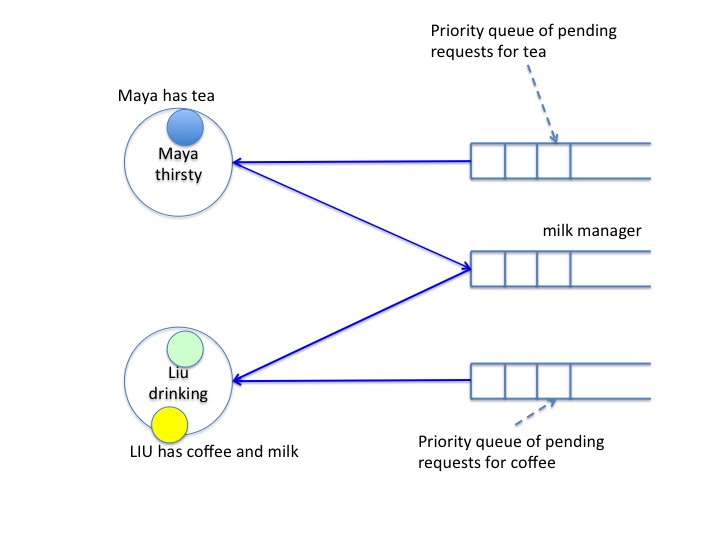
The example shows a scenario. The system has two agents, Maya and Liu both of whom are tranquil in the initial state. There are three beverages: Tea, coffee and milk. Initially, these beverages are with their managers.

The next diagram, stage 1, shows the state after Maya gets thirsty for tea and milk. So she sends requests to the managers of tea and milk. The priority of this request is 2. (We will discuss how priorities are obtained later.)

The next diagram, stage 2, shows the situation after the managers of tea and milk get requests from Maya, and respond by sending the beverages to Maya because there are no pending requests for these beverages. The beverages, tea and milk, are in the channel to Maya.

The stage 3 diagram shows a state after Liu becomes thirsty for coffee and milk. So she sends requests for coffee and milk to the managers of these beverages. The priority of the request is 5.

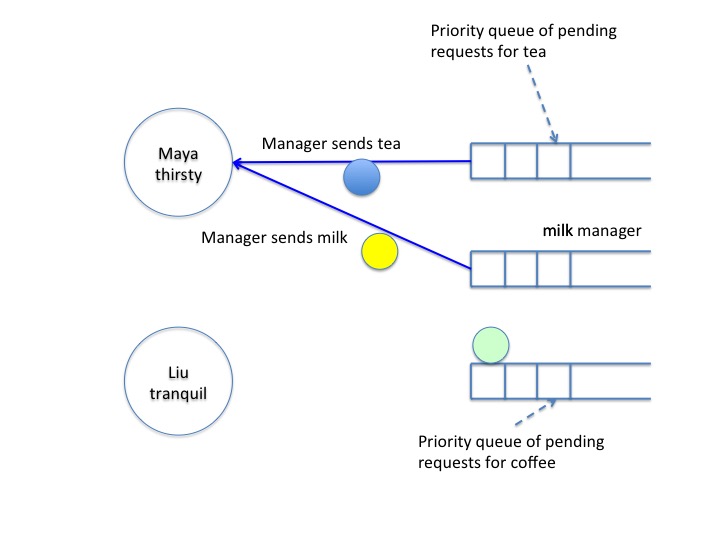
Maya has received the milk beverage but tea is still in the channel. So, Maya remains thirsty.

The stage 4 diagram shows a state in which the coffee manager receives Liu's request and sends coffee to Liu because there are no pending requests for coffee. When the milk manager gets Liu's request, the manager puts the request on the priority queue of pending requests. At this point the queue has only Liu's request. The milk manager demands milk back from Maya because her request has priority 2 whereas Liu's request has priority 5. Maya is still thirsty because the tea hasn't arrived yet.

Next, Maya receives the demand for milk and responds by sending the milk back to the milk manager. Maya also resends its original request for milk, with priority 2, to the milk manager. Then Maya receives tea. Maya continues to be thirsty because she has only one of the two beverages that she needs to drink. Liu has coffee, but she remains thirsty because milk is in the channel from Maya to the milk manager.

In stage 6, the milk manager has received Maya's request for milk with priority 2 and received milk. So, the milk manager sends the milk to respond to the highest priority request in the priority queue; this request is from Liu. The milk manager puts Maya's request into the queue of pending requests.

In stage 7, Liu has received both milk and coffee, and so she is drinking. Maya is still thirsty, holding tea, while Maya's request for milk is in the queue of pending requests for milk.

How Priorities Change

If priorities don't change then the agents with high priorities may continue to go rapidly through the tranquil, thirsty, drinking cycle while other agents remain thirsty for ever.

One way to assign priorities is as follows. Associated with each request is a timestamp which is the time read from the requestor's local clock at the instant at which the request is made. A request's timestamp does not change after the request is created.

A request's priority is a pair (timestamp, requestor's id), with priorities compared lexicographically, and lower values having higher priority. So, requests made earlier have higher priority than requests made later. The requestor's id is used to break ties.

What are the requirement's of agents' local clocks that ensure that all thirsty philosophers drink eventually?

A Minimum Requirement on Clocks

An agent's clock must tick forward between successive requests by the agent. If the agent's clock remained stuck at the same value for ever then the agent using that clock may get the highest priority for ever, and go through tranquil, thirsty, drinking cycles infinitely which makes other agents remain tranquil for ever.

Assume that each clock reading is an integer: for example, the number of picoseconds since January 1, 1900. (NTP units are \(2^{-32}\) of a second.) The clock ticks forward between successive requests by the same philosopher because the philosopher remains in tranquil state for at least \(\gamma\) units of time where \(\gamma\) is a positive constant. Treat each agent's clock tick as an event.

Local clocks of agents may drift apart, but let's assume that the magnitude of the difference between clock readings of different agents is bounded.

Even if the philosopher makes a new request when its clock ticks forward by one unit, eventually the timestamp of a request from that philosopher will exceed \(T\) for any value of \(T\). This ensures that while a philosopher is thirsty, another philosopher cannot overtake it for ever.

Proof of Correctness

The proof of safety --- multiple philosophers don't hold the same beverage at the same time --- is straightforward. It follows because a token is at exactly one agent or in exactly one channel.

Let's prove that a thirsty philosopher \(v\) with a request with timestamp \(T\) drinks eventually. Let \(t[i]\) be the reading of philosopher \(i\)'s clock.

Each agent's clock reading eventually exceeds \(T\)

We observe that each agent's clock ticks forward:

\( \forall i, \tau: (t[i] = \tau) \leadsto (t[i] \geq \tau + 1) \)

Therefore, each \(i\)'s clock eventually reads a value greater than \(T\), using transitivity of \(\leadsto\).

\( \forall i, \tau: (t[i] = \tau) \leadsto (t[i] > T) \)

From the previous formula, and taking disjunction over all values of \(\tau\):

\( \forall i: \quad true \leadsto (t[i] > T) \)

Because clock readings never go back in time, \(t[i] > T\) is stable, and therefore:

\( \forall i: \quad true \leadsto always(t[i] > T) \)

Let \(Q\) be the predicate that all clocks read values that exceed \(T\):

\(Q = \forall i: t[i] > T\).

From the above formula and because \(X \leadsto always(Y)\) and \(X \leadsto always(Y')\) allows us to deduce \(X \leadsto always(Y \vee Y')\)

\( true \leadsto always(Q) \)

The number of pending requests with timestamps less than \(T\) decreases

From the above formula:

\( v.thirsty \; \leadsto \; (v.drinking \wedge Q) \vee (v.thirsty \wedge Q) \)

Next we will prove that if \(v\) is thirsty and all clocks read values that exceed \(T\), then \(v\) will drink eventually:

\( (v.thirsty \wedge Q) \leadsto v.drinking \)

Let \(req\) be the number of pending requests with timestamps less than \(T\). We will prove

\( (v.thirsty \wedge Q \wedge (req = k) \; \leadsto \; v.drinking \vee (v.thirsty \wedge Q \wedge (req < k)) \)

This proof is straightforward: The request with the lowest timestamp gets all the resources it needs.

\( (v.thirsty \wedge Q \wedge (req = 0) \; \leadsto \; v.drinking \)

The result follows using the rules for variant functions.

Review

1. In the algorithm, each manager of a resource maintains a priority queue of requests for the resource. Is the algorithm correct if managers maintain first-come-first-served queues rather than priority queues?
2. Show that the proposed variant function is correct: show that it does not increase while an agent remains thirsty, and show that it decreases eventually.