Leads-To: Introduction

This module introduces the temporal logic concept of leads-to and its basic properties.

A message at the head of a channel from an agent \(A\) to an agent \(B\) is eventually delivered to \(B\). The message does not remain in the channel forever. The message at the head of the channel may be delayed for an arbitrary finite time, but is not delayed for infinite time. The concept of leads to captures the idea of a predicate holding "eventually."

Let \(P\) and \(Q\) be predicates. \(P \leadsto Q\) is a property of a system: a property is a boolean which either holds for the system or does not hold for the system. \(P \leadsto Q\) is read as \(P\) leads to \(Q\).

A trajectory is an infinite path through the state space which satisfies the condition that every message at the head of a channel is delivered eventually.

---

The property \(P \leadsto Q\) holds for a system exactly when any trajectory that visits a state in which \(P\) holds is at, or later visits, a state in which \(Q\) holds.

---

The interval between the point at which the trajectory visits \(s\) and the later point at which the trajectory visits \(s'\) is finite.

For example, consider a trajectory, which is an infinite sequence of states, \(S_{0}, S_{1}, S_{2}, \ldots\). If \(P\) holds in \(S_{i}\) and \(P \leadsto Q\) then there exists some \(j \geq i\) such that \(Q\) holds in \(S_{j}\). (Note that \(j\) could be equal to \(i\).)

Example

Consider a program

x = 0
while true:
    x = x + 1
    

For this program, for all \(i, j\) where \(j \geq i\): \((x = i) \leadsto (x = j)\)

Example

A system has agents \(x\), \(y\) and \(z\). There are channels from \(x\) and \(y\) to \(z\). Execution of actions on channels are fair: If a channel has a message then that message will be delivered eventually.

Agent \(z\) has a variable \(v\) which is initially 0. If \(z\) receives a message from \(x\) before receiving a message from \(y\) it sets \(v\) to 1. If \(z\) receives a message from \(y\) before receiving a message from \(x\) it sets \(v\) to 2. The initial state init of the system has one message on each channel from \(x\) to \(z\) and from \(y\) to \(z\).

Is the following true: \(init \; \leadsto \; (v = 1)\)?

No, because the message from \(y\) may arrive before the message from \(x\).

Is the following true: \(init \; \leadsto \; (v \leq 2)\)?

Yes, because messages from \(x\) and \(y\) will arrive eventually.

Example

Consider a program

x = 0
while true:
    x = x + 2

Does the following progress property hold for the system?

\( (0 \leq x \leq 1) \quad \leadsto \quad (x = 3) \)

No, because if \(x = 0\) then \(x\) never becomes \(3\). The definition of \(P \leadsto Q\) is that ALL paths from ALL states in which \(P\) holds eventually visit states in which \(Q\) holds.

Example

Does the following progress property hold for the system?

\( (0 \leq x \leq 1) \quad \leadsto \quad (2 \leq x \leq 3) \)

Yes. All paths from all states in which \(0 \leq x \leq 1\) eventually visit states in which \(2 \leq x \leq 3\).

Example

Does the following progress property hold for the system?

\( (0 \leq x \leq 1) \quad \leadsto \quad (2 \leq x) \)

Yes. All paths from all states in which \(0 \leq x \leq 1\) eventually visit states in which \(2 \leq x\).

Example

Does the following progress property hold for the system?

\( (0 \leq x \leq 1) \quad \leadsto \quad (0 \leq x \leq 1) \)

Yes. Any trajectory that visits a state in which \(0 \leq x \leq 1\) at a point \(T\) eventually visit states in which \(0 \leq x \leq 1\), because "eventually" includes the possibility of immediacy.

Example

A system has agents \(x\), \(y\) and \(z\). There are channels from \(x\) and \(y\) to \(z\). Agent \(z\) has variable \(xcount\) and \(ycount\) which are initially 0. When \(z\) receives a message from \(x\) it executes:

xcount = (xcount + 1) mod 10

and when \(z\) receives a message from \(y\) it executes:

ycount = (ycount + 1) mod 5

In the initial state \(xcount, ycount\) are both 0. Agents \(x\) and \(y\) send messages to \(z\) forever.

Is the following true: \(init \; \leadsto \; (xcount = 9)\)?

Yes

Is the following true: \(init \; \leadsto \; (ycount = 4)\)?

Yes.

Is the following true: \(init \; \leadsto \; (xcount = 9) \wedge (ycount = 4)\)?

No. The state in which \((xcount = 9) \wedge (ycount = 4)\) may never occur in a transaction.

Example

Same agent structure as the previous example. The program for agent \(z\) is as follows.When \(z\) receives a message from \(x\) it executes:

if xcount < 10:
   xcount = xcount + 1

and when \(z\) receives a message from \(y\) it executes:

if ycount < 5:
   ycount = ycount + 1

In the initial state \(xcount, ycount\) are both 0. Agents \(x\) and \(y\) send messages to \(z\) forever.

Is the following true?

\(init \leadsto (xcount = 10)\)

Yes. Is the following true?

\(init \leadsto always(xcount = 10)\)

Yes. Is the following true?

\(init \leadsto always(ycount = 5)\)

Yes. Is the following true?

\(init \leadsto always((xcount = 10) \wedge (ycount = 5))\)

Yes because eventually every trajectory that starts from \(init\) visits and forever thereafter remains in a state in which \((xcount = 10) \wedge (ycount = 5)\).

Example

What is the meaning of \(E(A(Q))\)?

A state \(s\) is in \(E(P)\) if and only if all trajectories that visit \(s\) visit a state in \(P\) at or after it visits \(s\).

Therefore a state \(s\) is in \(E(A(Q))\) if and only if all trajectories that visit \(s\) eventually visit and remain forever in states that satisfy \(Q\).

Example

Is the following true?

\( E(A(P)) \wedge E(A(Q)) \; \equiv \; E(A(P \wedge Q)) \)

A state \(s\) is in \(E(A(P)) \wedge E(A(Q))\) if and only if all trajectories that visit \(s\) eventually visit and remain forever in states that satisfy \(P\) and in states that satisfy \(Q\). Therefore if a state \(s\) is in \(E(A(P)) \wedge E(A(Q))\) then it is also in \(E(A(P \wedge Q))\) i.e.,

\( E(A(P)) \wedge E(A(Q)) \; \Rightarrow \; E(A(P \wedge Q)) \)

The converse,
\( E(A(P \wedge Q)) \; \Rightarrow \; E(A(P)) \wedge E(A(Q)) \)
is also true because \(E\) and \(A\) are monotonic functions, i.e. for any predicates \(R, R'\):

\( [R \Rightarrow R'] \wedge E(R) \quad \Rightarrow \quad E(R') \)

\( [R \Rightarrow R'] \wedge A(R) \quad \Rightarrow \quad A(R') \)

---

We will almost always prove progress by proving a formula of the form:

\( P \leadsto \neg P \)

---

which says that predicate \(P\) does not hold forever.

An example of such a formula is that a message \(M\) is at the head of a channel; that condition does not persist forever because the message will be delivered eventually.

One way of proving that \(P \leadsto \neg P\) is to identify an action \(a\) such that if \(a\) is executed in any state in that satisfies \(P\) then the state when \(a\) terminates satisfies \(\neg P\).

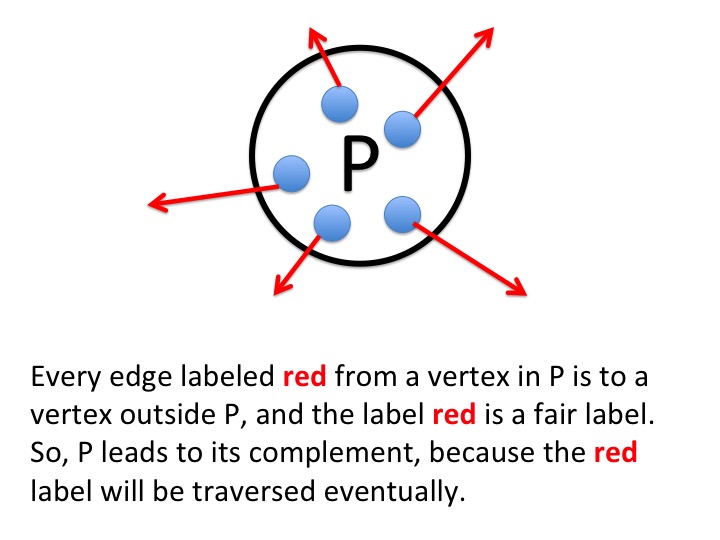
Formulae using Leads To

Transitivity of \(\leadsto\)

\( (P \leadsto Q) \wedge (Q \leadsto R) \; \Rightarrow \; (P \leadsto R) \)

If any trajectory that visits a state in which \(P\) holds, later visits a state in which \(Q\) holds in a finite number of steps, and any trajectory that visits a state in which \(Q\) holds, later visits a state in which \(R\) holds in a finite number of steps, then any trajectory that visits a state in which \(P\) holds, later visits a state in which \(R\) holds in a finite number of steps.

Disjunction left-hand side of \(\leadsto\)

\( (P \leadsto R) \wedge (Q \leadsto R) \; \Rightarrow \; ((P \vee Q) \leadsto R) \)

The proof is straightforward.

Basic Property of \(\leadsto\)

Let \(R = P \wedge \neg Q\).

\( (R \; \rightarrow \; (R \cup Q)) \wedge (R \; \leadsto \; \neg R) \quad \Rightarrow \quad (P \leadsto Q) \)

Proof outline: \(R \; \rightarrow \; (R \cup Q) \) implies that every trajectory from a vertex in \(R\) either (1) remains in \(R\) forever or (2) visits a vertex in \(Q\). But, \(R \leadsto \neg R\) implies that the first case is not possible. So, every trajectory from a vertex in \(R\) visits a vertex in \(Q\)

Trajectories from \(P \wedge Q\) are already in \(Q\), and therefore every trajectory from a vertex in \(P \wedge Q\) visits a vertex in \(Q\). The theorem follows from \(P = (R \vee (P \wedge Q) \)

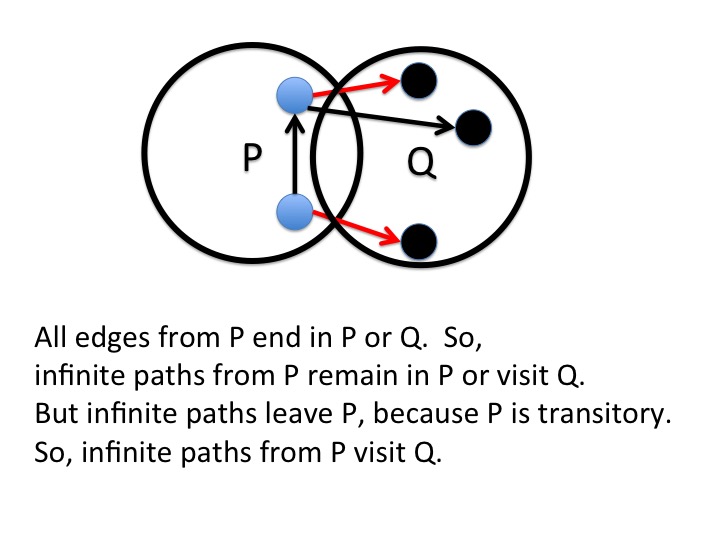
We call this property the basic property because it is the property on which most proofs of progress are based.

The left-hand side of \(\leadsto\) in the Basic Property has two parts:

1. Safety: \(R \; \rightarrow \; (R \cup Q)\) which deals only with a transition from a state to the next.
2. Progress: \(R \leadsto \neg R\) which says that \(R\) does not hold forever.

Variant Functions and \(\leadsto\)

We use variant functions extensively in proving progress.

Let \(f\) be a variant function. So \(f\) is a function from states of the system to a well-founded set. The following theorem is an extension of the basic property. Let \(P\) and \(Q\) be predicates

Variant Function Theorem

\(\forall K: \quad P \wedge (f = K) \; \leadsto \; (P \wedge (f < K)) \vee Q\)
\(\Rightarrow\)
\(P \leadsto Q\)

Proof

The left-hand side of the implication is the following leads-to formula: If \(P \wedge \neg Q\) holds and the value of the variant function is \(K\) in a state \(s\) then all trajectories from \(s\) enter a state in which: (1) \(P\) holds and the variant function value decreases or (2) \(Q\) holds.

Since the value of the variant function can decrease only a finite number of times it follows that

\( P \wedge (f = K) \quad \leadsto \quad Q \)

Take the disjunction of the left-hand side of the \(\leadsto\) over all \(K\) in the above equation to get: \(P \leadsto Q\).

Useful way of Proving Progress

A convenient and useful way of proving \(P \leadsto Q\) is to use the variant function theorem coupled with the basic property. This proof has two parts:

1. Safety: The variant function doesn't increase until \(Q\) holds.
2. Progress: Eventually the value of the variant function changes or \(Q\) holds.

The second part uses concepts about progress such as \(\leadsto\), whereas the first part only deals with transitions from a state to the next state.

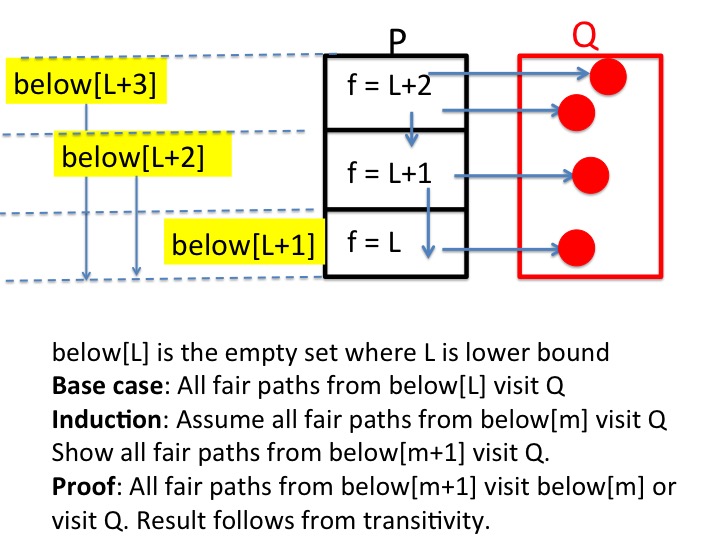
Variant function doesn't increase while \(\neg Q\) holds

\( (P \wedge (f = K) \wedge \neg Q) \; \rightarrow \; (P \wedge (f \leq K)) \vee Q \)

This formula says that if \(P \wedge \neg Q\) holds in a state where the value of the variant function is \(K\) then in the next state either (1) \(P \wedge \neg Q\) continues to hold with the same or lower value of the variant function or (2) \(Q\) holds.

Variant function cannot remain unchanged while \(\neg Q\) holds

Let \(R \; \equiv \; (P \wedge (f = K) \wedge \neg Q)\). Then:

\(R \leadsto \neg R\)

This formula says that \(R\) does not hold forever.

The variant function theorem follows from the two parts.

Summary of Proof Rules for \(\leadsto\)

1. To prove \(P \leadsto \neg P\), identify an action \(a\) which is executed infinitely often and for which the following Hoare triple holds: \(\{P\} \; a \; \{\neg P\}\).
2. Transitivity: If \(P \leadsto Q\) and \(Q \leadsto R\) then
   \(P \leadsto R\)
3. Disjunction: If \(P \leadsto Q\) and \(P' \leadsto Q\) then
   \((P \vee P') \leadsto Q\)
4. Basic Property: If \([\forall a: \; \{P\} \; a \; \{P \vee Q\}]\) and \(P \leadsto \neg P\) then
   \(P \leadsto Q\)

The use of the variant function uses all of these proof rules.

Eventually and CTL

We define an operator Eventually or \(E\) on predicates as follows: For a predicate \(Q\), \(E(Q)\) holds for a state \(s\) exactly when for every trajectory that starts in \(s\): \(Q\) holds in \(s\) or at a future point in the trajectory.

So \(E(Q)\) is the weakest predicate \(P\) such that \(P \leadsto Q\). Therefore

\( E(Q) \leadsto Q \)

and

\( (P \leadsto Q) \; \equiv \; [P \; \Rightarrow \; E(Q)] \)

The definition of Eventually in terms of CTL is \(E = AF\) where \(A\) stands for all trajectories from a state and \(F\) stands for a future point in the trajectory.

Summary

This module has properties that we use in proving the correctness of distributed algorithms.

---

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology