Introduction to Bitcoin

This module introduces the algorithm underlying BitCoin.

Bitcoin is based on cryptography and distributed consensus. We discussed aspects of cryptography required for Bitcoin in an earlier module. Next, we study the distributed consensus algorithm used by BitCoin. This Princeton University book has a superb (and longer) description of consensus in Bitcoin.

We discussed distributed consensus in the modules on Paxos and Byzantine Generals with written and oral messages. The specification of consensus is weaker in Bitcoin and the algorithm used to obtain consensus is different from those used in Paxos and Byzantine Generals written and oral algorithms. The Byzantine Generals algorithms assumes that the algorithm operates in rounds, whereas the Bitcoin algorithm doesn't require synchronous rounds in which all agents participate. The Paxos algorithm does not guarantee progress whereas Bitcoin requires progress with high probability; you wouldn't want to use coins if you had to wait a long time to buy anything.

No trusted agent

In an earlier module we described an algorithm that had many of the features that we expect from a cryptocurrency. That algorithm had, however, a characteristic which is problematic to some: It relies on a trusted agent. The trusted agent could be the Federal Reserve in the US or a central bank that manages a currency. Two of many reasons given for mistrusting banks are that (1) people may want to execute transactions in secret giving only their public keys, and (2) central banks may be able to print money whereas some cryptocurrencies, such as Bitcoin, limit the total amount of coins that can ever exist. The Bitcoin algorithm is a modification that eliminates the trusted agent from the algorithm given in the previous module.

No assumptions about numbers of agents

The Byzantine Generals algorithm uses an upper bound on the number of faulty agents. Paxos assumes that the total number of agents is known. The Bitcoin algorithm makes no assumptions about numbers of faulty and non-faulty agents other than that there are a large number of agents.

Incentives and transaction fees

When a currency is managed by a single trusted agent, such as a bank, we assume that the bank gets some reward for its service or is paid by a government to carry out this service. The Bitcoin algorithm pays agents with Bitcoins for checking the validity of transactions. This payment consists of new coins that are "mined". More about mining later

A First Proposal for an Algorithm

How can we modify the algorithm we described earlier so that it works without a trusted agent? Let's try this modification: Select random agents to play the role of the trusted manager.

A step of the algorithm is as follows: A single agent is chosen randomly to play the role of the trusted manager. This agent receives and validates transactions, gathers some of the transactions into a block, appends the block to the block chain, and broadcasts the updated block chain. The other agents update their copies of the block chain when they receive this value. The system waits for all agents to update their copies and then executes the next step.

Challenges of the Proposed Algorithm

This algorithm has several challenges.

1. Selecting a single agent. How can the collection of agents select a single agent to add a block to the block chain? The selection of a single agent requires all agents to reach a consensus about which agent to select. So solving the problem this way would require solving another consensus problem. The Bitcoin algorithm does not select a unique agent to add a block to the block chain; however, it uses an ingenious mechanism to ensure that multiple agents don't attempt to add blocks at about the same time.
2. Synchronization: How can the collection of agents wait long enough to ensure that all agents have updated their copies of the ledger to the most recent version before the ledger is modified again?

   Consider the following example scenario. All agents have the same copy x of the ledger at some point t. Agent B, selected randomly to act as the trusted agent, appends transaction y to the ledger at a later point t' at which point B's copy is [x, y]. Then, agent C, selected randomly to act as the trusted agent, appends transaction z to the ledger at a later point t''. If C's copy is still [x], because it has not as yet been updated to [x, y], then after C appends z to the ledger, C's copy becomes [x, z].

   ---

   A key property of the algorithm with the trusted agent is that two copies of the ledger are either identical or the longer copy consists of additional transactions appended to the shorter copy.

   ---

   With this property, two copies of the ledger are either identical or the shorter copy can eventually "catch up" to the longer copy by merely by appending more values.

   In the example, B may receive information about transaction z after receiving information about transaction y, whereas C may receive this information in the reverse order, which leaves B's copy as [x, y, z] and C's copy as [x, z, y]. In this case, the copies remain different forever.

   The Bitcoin algorithm does not guarantee synchronization; however, its mechanism helps to make many agents append blocks in the same order.

3. Incentives: Why should an agent chosen to play the role of trusted agent agree to play that role? What's the incentive? Why wouldn't the trusted agent do nothing at all execute its step slowly?
4. Untrustworthy Agents: The randomly-chosen trusted manager may not be trustworthy. You can imagine what may go wrong in the previous algorithm if the bank was dishonest.

Next, let's look at how the Bitcoin algorithm addresses challenges 1 and 2. We'll look at challenges 3 and 4 later.

Selecting a Single Random Agent

How can an arbitrary set of agents, some of whom may be malicious, and where the size of the set is unknown, pick a random agent?

Using Puzzles to Select a Single Agent

Let's look at a simple situation: several people solve puzzles in the same room. When a person solves her puzzle, she yells "I won!". When a person hears that somebody else has won she stops solving her puzzle.

If everybody starts at the same instant and take the same time then there will be collisions --- many will claim to win at the same time. If, however, the time to solve a puzzle is a random variable with a flat distribution then collisions are unlikely. Bitcoin uses the puzzle-friendly property of cryptographic hash functions discussed in the previous module.

Now, instead of people being all in the same room, assume that they are competing across a network. When a person solves a puzzle, she broadcasts a "I won" message. When a person working on a puzzle gets a "I won" message from somebody else, she stops working on her puzzle.

Collisions are likely if the expected time to solve the puzzle is small (say a millisecond) compared with the expected time (say a minute) for a message broadcast by one person to reach others. Message delays may cause multiple people to solve their puzzles before receiving "I won" messages. Collisions are unlikely when times to solve puzzles are much greater than message delays.

We could attempt to use timestamps: When a person solves her puzzle she broadcasts a "I won" message and the time at which she finished solving the puzzle. If a person gets a "I won" message with an earlier timestamp then she concedes. This approach is problematic because a devious agent may not solve the puzzle, or may set her timestamp to an earlier value.

Puzzles in Bitcoin

Next let's look at the puzzles used in Bitcoin. Each agent has its own copy of the block chain. An agent \(A\) collects a set \(trans\) of transactions that haven't as yet been added to \(A\)'s copy of the block chain. Agent \(A\) proposes to append a block to the chain where the block consists of the set \(trans\) in the following way.

Let \(ptr\) be the pointer to agent \(A\)'s copy of the block chain. Agent \(A\) can add a block containing \(trans\) to the chain only if it proves that it has solved the following problem --- the "puzzle."

Find a number, called \(nonce\), such that:

\(H(nonce + ptr + trans) < target \)

where \(+\) is the concatenation operator , and target is a given value.

For the time being assume that target is a constant; later, we'll see that it decreases very slowly over time. The smaller the value of target the greater the expected time to solve the puzzle.

The time to solve a Bitcoin puzzle is a random variable with a flat distribution. Each proposer of a block is probably solving a different puzzle because the block of transactions that it is aggregating is likely to be different from that of other proposers. Agents have different amounts of computing capacity, and the time to solve a puzzle decreases with capacity. Agents are unlikely to start solving their puzzles at the same instant. For these reasons, it is possible, but unlikely, that many agents will solve their puzzles at the same time.

Using puzzles to identify a single random agent leaves us with at least three challenges: (1) Collisions will occur; (2) agents may be devious --- they may claim to have solved puzzles when they haven't; and (3) agents with computing power that far exceeds those of others will solve their puzzles faster than others do --- and so though agents are selected randomly, those with large computing power are likely to be selected more often.

Attempts at Synchronization

When an agent \(A\) appends a new block \(B\) to a block chain \(L\) it broadcasts the new chain \(L + B\). This is analogous to a person shouting "I won" in the example given earlier.

When a (non-devious) agent \(A'\), which proposes to extend chain \(L\), gets a message saying that \(L\) has already been extended to \(L + B\) then \(A'\) stops attempting to append a block to \(L\). Instead, \(A\) starts again with a new set of transactions that it proposes to append to the extended chain \(L + B\).

If the message delay between agents \(A\) and \(A'\) is small compared to the time to solve puzzles, then a collision between \(A\) and \(A'\) is unlikely, but still possible. So, it is possible that \(A\) broadcasts \(L + B\) while \(A'\) broadcasts \(L + B'\) at about the same time. So different agents may have different copies of the block chain. What is the equivalent of the "true" system-wide block chain when different agents have different copies?

The Bitcoin algorithm does not use synchrony to deal with this issue. The problem of different copies of the block chain extant at the same time is handled in an ingenious asynchronous way that we describe later.

Managing Concurrent Updates

A key step of the Bitcoin algorithm that updates local copies of block chains is as follows. After an agent creates a block and appends the newly created block to its local copy it broadcasts its copy of the block chain.

---

When an agent \(A\) gets a message containing a copy of another agent's block chain, agent \(A\) sets its local copy to the block chain in the message if and only if the length of the block chain in the message exceeds the length of \(A\)'s local copy.

---

Let's look at a scenario. For this scenario, \(X\) and \(Y\) are single blocks. Assume that agent \(A\)'s copy of the block chain is \(L\) when \(A\) receives a message containing the block chain \(L + X\). Because the length of the block chain \(L + X\) is bigger than \(A\)'s copy, \(A\) sets its copy to \(L + X\).

Now suppose agent \(A\) gets a message containing the block chain \(L + Y\); what does \(A\) do? Agent \(A\) ignores the message because the length of \(L + Y\) does not exceed that of \(A\)'s current copy, \(L + X\).

Continuing Collisions

Let's continue the above scenario. Can block \(Y\) become part of \(A\)'s chain, or will it remain forever an "orphan" block as far as \(A\) is concerned?

Here's a possible scenario. An agent with a block chain copy \(L + X\), solves its puzzle and appends a block \(X_{1}\) to get a new copy \(L + X + X_{1}\) of the block chain which the agent broadcasts. At the same time, another agent with a block chain copy \(L + Y\), solves its puzzle and appends a block \(Y_{1}\) to get a new copy \(L + Y + Y_{1}\) which is broadcast. If \(A\) receives \(L + Y + Y_{1}\) before receiving \(L + X + X_{1}\) then \(A\) will set its chain to \(L + Y + Y_{1}\), and then reject \(L + X + X_{1}\).

You can construct a scenario with a sequence of collisions between agents appending blocks \(X_{i}\) and other agents appending blocks \(Y_{j}\) so that \(A\)'s chain switches back and forth between \(X\) and \(Y\) values.

Long sequences of collisions are unlikely, and the longer the sequence the less the probability of continuing collisions.

So how can an agent determine whether a block is in the chain? And so how can an agent find out if a transaction has been executed? You sell your used bicycle to somebody for coins, but how do you know if that transaction becomes part of the block chain when different agents have different copies? And so how do you know that you can spend those coins that you should have received for your bicycle?

Confidence that a Block is in the Chain

In this section we discuss the behavior of non-devious agents; we will show how the algorithm handles devious agents later. Suppose an agent's copy of the block chain is \(X + X_{1} + X_{2} + \ldots + X_{K}\), and another agent's copy is \(Y + ? + ? + \ldots\), where \(?\) represents arbitrary values. What is the likelihood that \(Y \neq X\)?

\(Y\) can be different from \(X\) only if there are a sequence of \(K\) or more collisions. And the likelihood of a sequence of collisions decreases with \(K\). Likewise, the likelihood that an agent never receives a block chain containing \(X\) decreases with time, and so decreases with \(K\). So, if \(K\) is large then with very high probability, \(X\) is part of every agent's block chain.

Now suppose an agent's copy of the block chain is \(L + X + X_{1} + X_{2} + \ldots + X_{K}\). What is the likelihood that another agent's copy is \(L + Y + ? + \ldots\) where \(L\) is an arbitrary sequence? By the same argument, when if \(K\) is large then with very high probability, \(X\) is part of every block chain.

For practical purposes, many agents assume that if \(K > 6\) then \(L + X\) is a prefix of most agents' block chains. See the Princeton Bitcoin book.

Suppose agent \(A\) gets \(N\) Bitcoins in transaction \(X\). If \(K = 0\) then an agent can't be confident that \(A\) ever received these coins because this transaction may not persist in the block chain. As \(K\) increases agents become more confident that the transaction is in the block chain and that \(A\) did, indeed, receive these coins.

What happens to Orphan Transactions?

An agent may append a block \(Y\) to its chain, and this block may be dropped from the chains of all agents and never reappear after some point. We saw a scenario in which this happens. Such a block is an "orphan," because no agent has a record of that transaction after some time. If an orphan block contains the transaction in which you sold your bicycle in exchange for coins, then will you ever be able to spend your coins? Yes, you will get your coins as we see next.

Agents aggregate transactions that have not appeared in the agent's block chain into blocks and propose to append these blocks to the chain. A transaction that does not appear in block chains will be agrregated eventually by some agent and inserted into a block in the chain. Though the orphan block disappears the transactions in the block do not.

Incentives

Next, looks look at challenge number 3. Why should an agent create blocks of validated transactions?

Because the agent gets paid! Payment is from either a block reward or transaction fees.

Block rewards

An agent that creates a block gets a specified number of Bitcoins for itself as a reward called a block reward. The Bitcoins in a block reward are created by making the block; these Bitcoins don't exist until the block is created. The process of making blocks and acquiring block rewards is called "mining." Mining is the only way of creating new Bitcoins.

When Bitcoin started the reward for creating a block was 50 Bitcoins. The reward halves after the creation of a certain number (210,000) of blocks. The reward was reduced to 25 in 2013 and to 12.5 in 2018. Block rewards will vanish at some point in the future. The total number of Bitcoins that can ever be created has an upper bound: about 21 million.

(Bitcoins can be lost. An agent may lose the hash pointer to the transaction that gave the agent ownership of the coin, or an agent may lose its private key.)

Even when block rewards vanish, miners will continue to mine provided that they get paid transaction fees. A transaction fee is a payment by payers and payees to miners. Transaction fees are voluntary. A high-fee for a transaction is an incentive to miners to put this transaction into a block quickly. So, it's possible that agents that offer no fee or low fees may have to wait longer for their transactions to enter the block chain.

Incentives are critical for Bitcoin. Miners get paid to get their blocks into the long-term "consensus" block chain. Miners have an incentive to police the block chain because they don't get paid for appending erroneous blocks. If a miner appends an erroneous block to the chain then other miners won't extend chains containing the erroneous block, and so the erroneous block will become an orphan.

Any agent can check whether its copy of the block chain is valid; however, agents making ordinary transactions don't need to do so because there are many miners each of whom has an incentive to ensure that the block chain is legitimate.

Attacks

Next, looks look at challenge number 4.

Stealing coins

Can an agent steal a coin from an agent \(X\) by appending a block to the chain where the block contains a transaction in which \(X\) gives coins to \(Y\)?

No, this can't happen thanks to cryptography. A transaction into which \(X\) puts coins is valid only if \(X\) signs the transaction. \(Y\) cannot forge \(X\)'s signature, and so \(Y\) cannot create blocks that contain such fraudulent transactions.

Double spend

Can an agent spend the same coin twice? Can an agent buy something without paying for it?

Consider the following transaction using conventional checks issued by banks. A buyer gives a seller a check for $\(100,000\) for a house. The house is put in escrow. When the check clears and the seller receives the payment the buyer gets possession of the house. The legal process that includes notaries, real estate agents, and banks, helps ensure that the transaction concludes correctly or is aborted correctly.

Next, let's look at a transaction in which a person buys a video online by paying the seller Bitcoins. The buyer and seller know each other by their public keys and by their online addresses. The buyer broadcasts the transaction in which the buyer gives the seller the payment in Bitcoins. The amount is specified as a pair (transaction id, array index) described in the section pay transactions in the module introducing crypto currencies.

A miner puts the transaction into a block \(X\); appends the block to its copy \(L\) of the block chain; and broadcasts the extended block chain \(L + X\). When the seller gets a copy of the block chain \(L + X\), the seller concludes that it has received the payment from the buyer because the transaction has been recorded in a block chain. So the seller gives the video to the buyer.

The buyer cheats. The buyer creates a transaction in which the buyer transfers the same Bitcoins to the buyer itself. A miner creates a block \(Y\) that includes this transaction. A miner who has only received block chain \(L\) (and hasn't yet received chain \(L + X\)) appends \(Y\) to \(L\) to get a chain \(L + Y\), and broacasts \(L + Y\).

Now we have a situation in which one miner broadcasts a legitimate block chain \(L + X\) and a different miner broadcasts a legitimate block chain \(L + Y\). Both chains have the same length. A miner with chain \(L + X\) does not know at this point that another minder has chain \(L + Y\). So, miners will extend both block chains. (Note that the algorithm will not permit chains \(L + X + Y\) or \(L + Y + X\).)

We've seen this situation before: look at block collisions described earlier in this module. Both block chains will be extended, but eventually, with very high probability, one of the blocks \(X\) or \(Y\) will drop out of chain.

How should sellers protect themselves?

What is the equivalent of the buyer's check clearing in the bank?

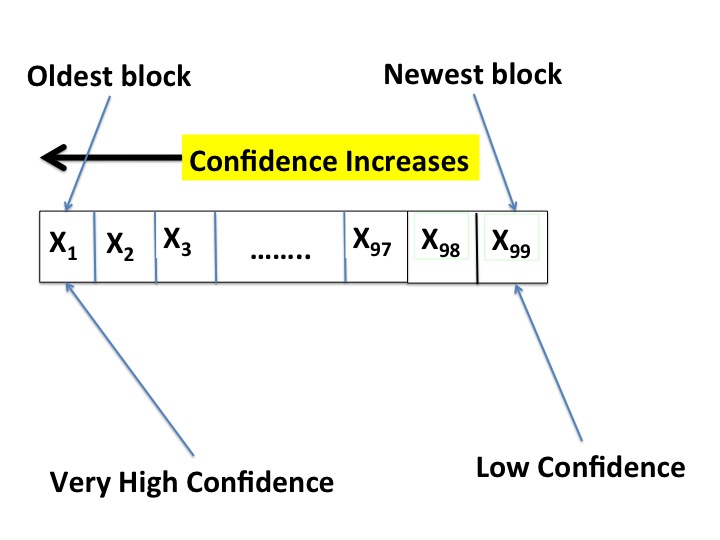
A seller should give the item to the buyer only after the transaction appears with high confidence in a block in the chain --- see Figure 1. The seller listens to block chains broadcast by miners. If the seller gets a block chain \(L + X + L'\) where \(L'\) is itself a long block chain then the seller has high confidence that the transaction is in the permanent record.

The seller waits to get block chains in which its transaction appears in a block which is then followed by \(m\) blocks, for large \(m\). The larger the value of \(m\), the greater the seller's confidence, but the longer the buyer has to wait to get paid. length of the extension \(L'\). A value of \(m = 6\) gives adequate confidence in most cases.

Fraudulent miners

A miner gets paid for every block the miner creates; so, why shouldn't the miner create fraudulent blocks and get paid for them?

The answer is the same as that for the double-spending attack. A miner may have created a block and appended it to the chain; however, a suspicious agent (and we hope that all agents are suspicious!) will not accept the block until many blocks have been appended to the chain after it. Other miners won't append their blocks to an invalid one. The invalid blocks will become permanent orphans, and so the fraudulent miner won't be able to spend the coins in these blocks.

Fifty One Percent Attacks

A 51% attack can be carried out by an agent that has more mining power (e.g. 51% or more) than all other agents combined. The higher the proportion of mining power of a single agent, the greater the chances that attacks by that agent will succeed. You can see the danger of a single agent having predominant mining power by thinking about an agent with say, 99% of the total mining power. This agent can mine so much faster than others that it can manipulate the block chain in many ways. It can create double-spend transactions and deny services to some transactions.

A group of miners can collude to gain predominant mining power. Also, miners can rent Cloud-based systems for mining --- as opposed to having to own huge data centers. An attacker can rent a large system for the specific purpose and duration of an attack. The public may not know if and when such attacks are successful because cryptocurrencies do not have an incentive to publish such attacks.

Denial of service

Can agents collude so that an agent \(X\)'s transactions never get into blocks and so never get processed?

An agent's identity does not appear in a transaction, only a public key does. An agent can create new public keys at will. So let's ask another question: can agents collude so that transactions with a specific public key do not get into blocks?

Only an agent that can solve puzzles in reasonable time can make blocks. These agents have significant computational power. One can concoct a situation where many agents with significant computation power collude to avoid transactions from a specific public key. This could have the effect of slowing processing of certain transactions. However, such a situation isn't likely to arise because agents have an incentive to create blocks and so they compete --- rather than collude --- with each other. Colluding agents, with massive computing power, may help to deny or slow service to a public key but not to another agent because agents can create public keys at will.

Further Reading

There are many issues that we have not covered. This material only covers the basics from the point of view of distributed algorithms.

Review

1. What is a block chain?
2. How does the algorithm deal with the situation in which one agent receives a message to extend its copy of the block chain with a block \(X\) while another agent receives a message to extend its copy of the block chain with a different block \(Y\)?
3. Could there be an infinite sequence of collisions? Is that likely?
4. What is mining for cryptocurrency? Suppose only a small number (say two organizations) mined most (say 99%) of Bitcoins. Would that be a problem?
5. Why is double spending unlikely to be successful?