Cryptography for Cryptocurrency

This page is a review of elementary cryptographic operations and introduces a simple cryptocurrency managed by a trusted agent.

The next module discusses the algorithm underlying Bitcoin; the Bitcoin algorithm doesn't require agents to be trusted. This Princeton University book is a superb description of Bitcoin.

Review: Cryptographic Hash Function

A hash function, \(H\), maps input strings of arbitrary size to outputs of fixed size.

Collision Resistance

Input values \(x, y\) of a hash function \(H\) are said to collide when \(H(x) = H(y)\). A hash function \(H\) is said to be collision resistant if the only known ways of finding collisions using the hash are intractable.

Let's look at the following problem: Given \(H\), find any colliding pair \(x, y\).

Consider a hash function \(H\) that outputs \(n\)-bit numbers and whose input is \(m\) bit strings. As a specific example lets assume that \(m\) is a large number and \(n = 4\). We can find a collision in the following way.

Let \(D\) be an array of size \(2^{n} = 16\). Initially \(D\) contains null values. Repeat the following iteration until a collision is found. Pick a random input \(x\). If \(D[H(x)]\) is null then set \(D[H(x)] = x\) else there is a collision between \(H(x)\) and \(x\).

By the pigeon-hole principle, we will find a collision in at most \(2^{n} + 1 = 17\) iterations. This brute-force algorithm uses space \(2^{n}\) and finds a collision in at most \(2^{n} + 1\) steps. From the Birthday Paradox a collision will be found with high probability in \(2^{n/2}\) iterations though the worse-case time is \(2^{n}+1\). If \(n = 256\) then a collision will be found with high probability in \(2^{128}\) iterations; however, executing \(2^{128}\) steps is still intractable.

For \(H\) to be collision resistant the output of \(H\) must be \(n\)-bits for large \(n\). For example \(n = 256\) in the SHA-256 hash function.

Commitment using Hashes

You bet that your soccer friend, Megan, cannot predict the winner of the 2022 World Cup. Megan puts the name of the predicted winner, \(W\), in an envelope and gives it to a trusted third party. After the World Cup is over, the third party reveals Megan's prediction, and at that point you can find out whether Megan's prediction was accurate.

The trusted third party provides two services:

Hiding: You can't find out Megan's prediction until the third party reveals it.
Binding: Megan can't change her prediction after giving it to the third party.

Can we use a hash function instead of a trusted third party?

Hiding

Let's try the following idea. Megan commits to \(W\) in the following way. She announces a hash function, \(H\), and the hash, \(y\), where \(y = H(W)\). You know \(H\) and \(y\). After the World Cup is over, she reveals her prediction, \(W\). At this point you can verify that \(y = H(W)\).

Does the hash function provide the services of the third party? Can you discover Megan's prediction before she reveals it?

It's easy. There are only 32 teams playing. Compute \(H(x)\) where \(x\) runs over each of the 32 teams. One of those teams has to be \(W\). You can discover her prediction in at most 210 steps.

Let's try another algorithm. Megan selects a secret value \(r\) which she keeps to herself. Instead of giving you \(H(W)\), she gives you \(y\) where \(y = H(r + W)\) and where \(+\) indicates concatenation of strings. Can you discover \(W\) from \(H\) and \(y\) without knowing \(r\)?

A brute-force solution is to try every combination of \(r\) and \(W\). If \(r\) is obtained from a distribution that is spread out, then finding \(W\) without knowing \(r\) take so much time that it is practically impossible.

Hiding: Given \(H, y\), where \(y = H(r + W)\) and \(r\) is a secret, discovering \(W\) is intractable.

Binding

Does the hash function \(H\) and the secret \(r\) provide both services of the trusted third party? Is Megan bound to her prediction or can she change her "prediction" after knowing the winner of the World Cup?

Suppose Megan has values \(r\) and \(r'\) such that H(r + 'Brazil') = H(r' + 'Italy'). After the World Cup is over, she can announce that her secret is \(r\) if Brazil wins, and announce that it is \(r'\) if Italy wins.

A hash function \(H\) is binding if finding pairs \((x,y)\) and \((x',y')\) where \(y \neq y'\) such that: \(H(x + y) = H(x' + y')\) is intractable.

Suppose you give Megan a hash function that is binding. Then she cannot find (in reasonable time) values \(r_{j}\) to match country \(C_{j}\) such that

\(H(r_{0} + C_{0}) = H(r_{1} + C_{1}) = H(r_{2} + C_{2}) = \ldots\).

and so she can't wait for the winner \(C_{j}\) to be announced before announcing her secret \(r_{j}\).

In summary, we can use a hash function that is hiding and binding to play the role of a trusted third party in a commitment.

Puzzle Friendly

The concept of puzzle friendly is related to hiding. Let \(r\) be a value picked from a spread-out distribution. Let \(H\) map arbitrary length strings to \(n\)-bit strings. Consider the following problem: Given \(H\), \(r\), and an \(n\)-bit value \(y\), compute any \(x\) such that \(H(r+x) = y\).

In this problem, as opposed to the hiding problem, we are given \(r\) and not \(x\),

The hash function \(H\) is said to be puzzle friendly exactly when any algorithm to solve this problem is about as slow as a brute-force algorithm which checks \(H(r+x) = y\) for random values of \(x\). The number of steps taken by any algorithm that solves this problem is not significantly lower than \(2^{n}\).

Now, let's look at the following related problem. Given \(H\), \(r\), and a set \(Y\) of \(n\)-bit strings, compute any \(x\) such that \(H(r+x) \in Y\). If \(Y\) consists of a single element \(y\) then this problem is the same as that in the previous paragraph. If \(Y\) is a set of all \(n\)-bit strings then this problem is trivial because any \(x\) solves the problem. The probability that a random value hashes to an element of \(Y\) is proportional to the cardinality of \(Y\). The cardinality of \(Y\) controls the expected time to solve the puzzle.

The hash function \(H\) is puzzle friendly when given \(H\), \(r\), and a set \(Y\) of \(n\)-bit values, the time required to compute any \(x\) such that \(H(r+x) \in Y\) is not significantly lower than \(2^{n} / |Y|\), where \(|Y|\) is the cardinality of \(Y\).

A Cryptographic Hash Function

A cryptographic hash function is one that is collision resistant, hiding and puzzle-friendly.

Hashing Inputs of Arbitrary Length

Let \(f\) be a function that operates on input strings of fixed length and produces output strings of fixed length. Let the input and output strings of \(f\) have lengths \(M + N\) and \(M\), respectively. We look at functions where \(N > 0\), and since the output is smaller than the input, \(f\) is called a compression function.

We can use function \(f\) to define a function \(g\) whose inputs are strings of arbitrary lengths and whose outputs are strings of length \(M\). Example code for \(g\) is given below where InitialValue is a given constant string of length \(M\).

def g(y):
    output = InitialValue

    // pad y so that it's length is a multiple of N
    if len(y)%N > 0:  y = y + "0"*(N - len(y)%N)

    // partition y into blocks of size N
    blocks = [y[i: i+N] for i in range(0, len(y), N)]

    // Apply function f to the concatenation of the
    // previous output (length M) with each block
    // (length N) to get the next output (length M).
    for block in blocks: output = f(output+block)
    return output

Hash Pointers

A hash pointer to an item \(D\) of data is a pair \((ptr, H(D))\) where \(ptr\) is a pointer that points to \(D\), and \(H\) is a cryptographic hash function.

Any data structure with pointers can be converted into a data structure with hash pointers: merely replace a pointer \(ptr\) to \(D\) by \((ptr, H(D))\).

Tamper-Evident Data Structures

Single Block

A simple example of a tamper-evident structure is a single block of data D which is pointed to by a hash pointer consisting of a regular pointer and a hash H(D).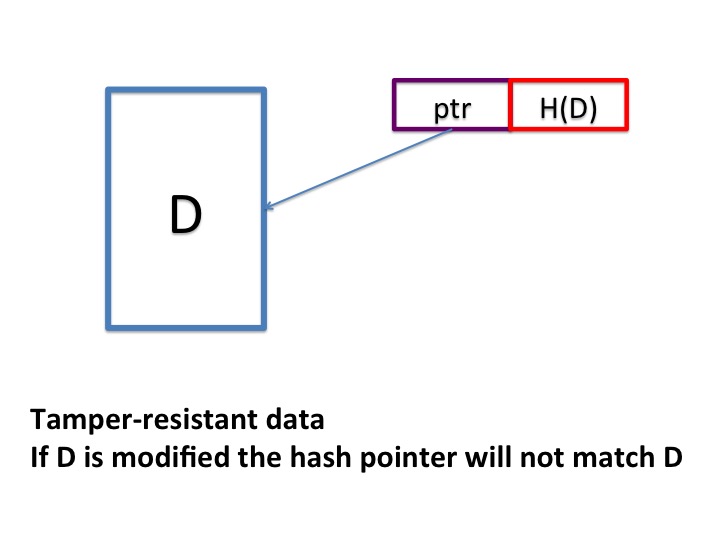

Fig1 — Fig.1: Hash Pointer points to a Tamper-Evident Block of Data

Assume that a malicious agent cannot modify both the hash pointer and the data that it points to. If an agent changes D to D' then the tampering can be discovered because the hash pointer won't match the data that it is pointing to: \(H(D') \neq H(D)\).

Tamper-Evident Linked List

Let's look at linear linked list to which elements can be appended but not deleted. The \(i\)-th element appended to the list points to the \((i-1)\)-th element. Let's replace the pointers in the list by hashed pointers.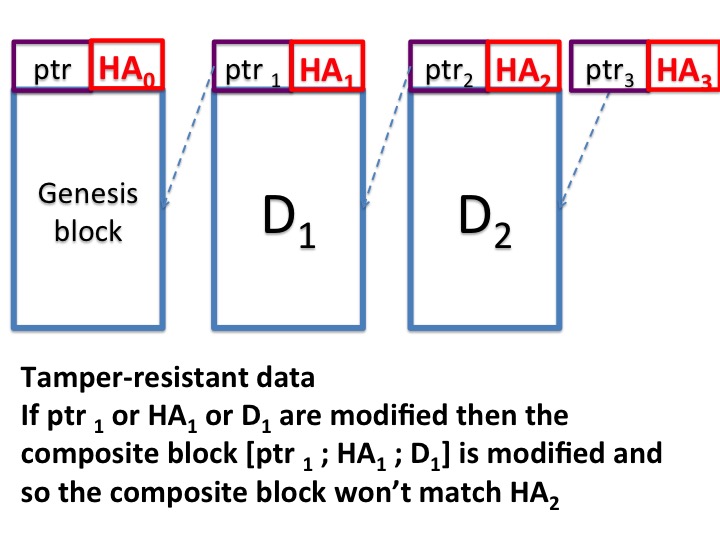

The \(j\)-th element of the list, \(j > 0\), consists of data, \(D_{j}\), and a hash pointer that points to the \(j - 1\)-th element of the list. The hash pointer in the \(j\)-th element consists of a regular pointer, \(ptr_{j}\), which points to the \(j - 1\)-th element of the list, and a hashed value, \(HA_{j}\), which is a cryptographic hash of the entire \(j-1\)th element consisting of \(D_{j-1}\), \(ptr_{j-1}\) and \(HA_{j-1}\). The \(0\)-th element is called the genesis element and has default values. The list is accessed by a hash pointer that points to the last element of the list; let this pointer be \(ptr_{n}, HA_{n}\).

Assume that agents cannot modify \(ptr_{n}, HA_{n}\). Then, can any agent determine whether the list has been tampered with?

Suppose the agent modifies \(D_{j}\), \(ptr_{j}\) or \(HA_{j}\) for any \(j < n\). Any agent can detect this tampering because the hash value \(HA_{j+1}\) will no longer match the \(j\)-th element of the list. If the malicious agent also modifies \(HA_{j+1}\) then hash value \(HA_{j+2}\) will no longer match the \(j+1\)-th element.

By induction on \(j\), any agent can detect tampering with the list provided malicious agents do not also modify the hash pointer to the last element of the last.

Tamper-Evident Acyclic Graphs and Merkle Trees

The idea described in the previous paragraph to convert linear linked lists can be used to convert directed acyclic graphs, in which nodes are connected by pointers, into tamper-evident graphs. A specific case of a directed acyclic graph is a rooted tree.

A Merkle tree is a special case of a binary balanced tree in which data items are stored only in the leaves. Nodes that are not leaves contain only hash pointers to nodes in the next level down. To prove that an element at the leaf is a member of the tree we need only the \(log_{2}(n)\) hash pointers on the path from the root to that leaf. By contrast, to prove that an element is a member of a linear list we need to inspect \(O(n)\) elements, on average.

Keys and Signed Messages

You can create a random public-key, private-key pair by calling a function on your computer. With high probability, nobody else has this specific pair of keys. Each individual's private key is a secret held by that individual. Public keys are accessible by everybody.

Sending messages securely

Keys are used to send messages securely. Kamala sends a secure message to Joe by encrypting the message with Joe's public key; Joe decrypts the message using Joe's private key. An agent cannot decrypt the encrypted message without Joe's private key.

Signing messages

Suppose Kamala needs to send a signed message to Joe while ensuring that nobody can forge her signature. She encrypts the message M with her private key to get an encrypted message M', and sends the pair (M, M') securely to Joe, i.e., she encrypts (M, M') with Joe's public key, and sends the resulting encrypted message to Joe. When Joe receives the message, Joe decrypts it using his private key to get (M, M'). Then Joe decrypts M' using Kamala's public key to get the decrypted message M''. If M'' = M then Joe knows that Kamala sent M because only an agent with Kamala's private signature could have sent that message.

Cryptocurrency Managed by a Trusted Agent

Let's start with a digital currency managed by a trusted agent that we will call a bank. Later, we will look at a consensus algorithm --- very different from Paxos and Byzantine Generals --- which will allow cryptocurrencies without trusted agent.

The bank maintains a tamper-evident linear list `L` of transactions that we call a tamper-evident ledger. Any agent can get a copy of the ledger. This tamper-evident ledger is the foundation of the currency.

A transaction is one of two types: create or pay. In a pay transaction, payers give coins that they possess to payees. An agent can be both a payer and payee of the same transaction. In a create transaction the bank creates coins that it gives to agents --- the payees of the transaction; the bank acts as the payer.

For this system to be trusted the bank must follow some protocol that determines how and when the bank creates coins. We won't discuss these protocols.

A pay transaction is signed by all payers of the transaction. A create transaction is signed by the bank. We discussed digital signatures and keys earlier.

Each element of the tamper-evident ledger has:

a unique id;
the type of the transaction, either create or pay;
list of payers: only for pay transactions --- a list indicating the agents who pay coins into the transaction and the amounts that they put in;
array of value-payee pairs: for both create and pay transactions --- an array of pairs (value, payee public key), where each pair in the array indicates that coins of the specified value are given to the payee with the specified public key.

Example of a create transaction

An example of a create transaction is:

(3146, create,  [(2.1, 7xxxx...), (3.2, 8xxxx)]).

The id of this transaction is 3146, the type of the transaction is create, and the array of value-payee pairs is

[(2.1, 7xxxx...), (3.2, 8xxx)]

In this transaction the bank creates a coin of value 2.1 and gives it to the agent with public key 7xxxx..., and the bank also creates a coin of value 3.2 and gives it to the agent with public key 8xxxx...

The pair:

(transaction id, index into array of value-payee pairs)

uniquely identifies a (value, payee) tuple.

For example (3146, 0) --- transaction id 3146, and array index 0 --- identifies value-payee[0] of transaction 3146 which is specified by the 2-tuple: (2.1, 7xxxx...). So, the transaction id and index, (3146, 0), tells everybody that the agent with public key 7xxxx received 2.1 units of coin in transaction 3146.

When this transaction is in a tamper-evident ledger, every agent from that point onwards knows that agent 7xxxx received 2.1 coins. Any modifications of this record can be detected.

Likewise, (3146, 1) --- transaction id 3146, and array index 1 --- identifies value-payee[1] which is the 2-tuple (3.2, 8xxxx...).

Pay transaction

Coins are transferred from payers to payees in a pay transaction.

Coins flowing into a pay transaction from payers

The payers are identified by a list of 2-tuples, where each 2-tuple is

(transaction id, index into array of value-payee pairs)

where transaction id is the id of the transaction in the tamper-evident ledger. As we said earlier, this pair uniquely identifies an agent and a value that this agent acquired in this transaction. For example the pair --- transaction id, index --- such as (3146, 0) identifies the 2-tuple (2.1, 7xxxx...); this 2-tuple asserts that the agent with public key 7xxxx received 2.1 units of coin in transaction 3146. The entire amount specified in the 2-tuple (2.1 in our example) is value that flows into this pay transaction from the agent with public key 7xxxx.

Suppose the payers in a pay transaction are identified by the list:

[(3146, 0), (7359, 3)]

and suppose pair 3 in transaction 7359 is (3.2, 8xxxx). Then the total amount of coins flowing into this pay transaction is 2.1 + 3.2, and this amount is disbursed to payees.

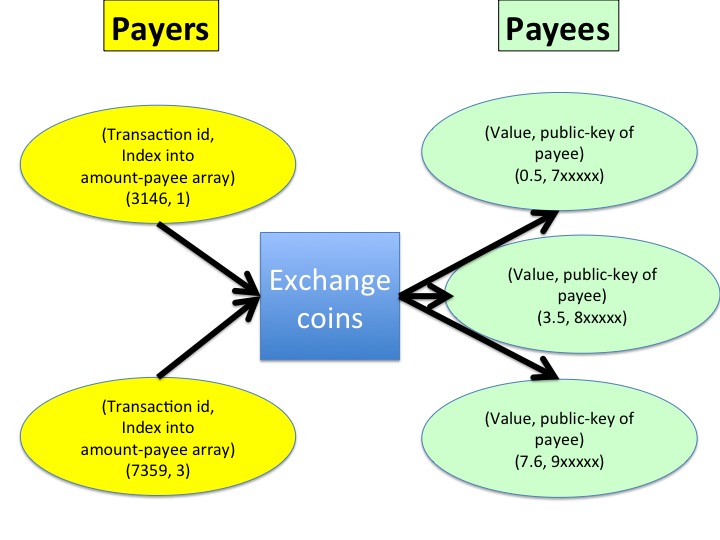
Coins flowing out of a pay transaction to payees

The outflow of coins is specified by an array of value-payee pairs, exactly as in a create transaction. The transaction clears all coins: the total inflow from payers is equal to the total outflow to payees in a transaction.

The system may provide incentives, such as payment of coins, to managers (e.g. banks) of cryptocurrencies. In this case, one of the payees is the bank itself.

Managing amounts spent in a transaction

A transaction-id, index pair --- such as (3146, 0) identifies a 2-tuple such as (2.1, 7xxxx...); this 2-tuple asserts that the agent with public key 7xxxx received 2.1 units of coin in transaction 3146. The entire amount specified in the 2-tuple (2.1 in our example) is value that flows into the transaction. What should this agent do if it wants to put in more than 2.1 coins into the transaction? Or less than 2.1 coins?

To put in more value, the bank identifies other transaction-id, index pairs in which this agent received coins. For example, say that (4539, 2) identifies a 2-tuple (3.2, 7xxxx), and assume that the payers in this transaction are specified by the pairs (3146, 0) and (4539, 2). The pair (3146, 0) asserts that agent (7xxxx) received 2.1 coins and the pair (4539, 2) asserts that the same agent received 3.2 coins. So the total amount of coins flowing into this transaction from this agent (7xxxx) includes 2.1 + 3.2.

To put in less value, the agent acts as both payer and payee; the net value that this agent pays out to other agents is the difference between the amount that this agent puts in and takes out. For example, if agent with public key 7xxxx wants to put in 1.9 coins into this transaction its payer information can be given by the transaction-id, index pair (3146, 0) which asserts that the agent received 2.1 coins and the same agent is a payee that withdraws 0.2 coins.

Preventing Double Spending

How does the system prevent an agent from using the same coin twice?

For example, the transaction id, index pair (3146, 0) identifies the 2-tuple (2.1, 7xxxx...); this tuple asserts that the agent with public key 7xxxx received 2.1 units of coin in transaction 3146. Why can't the agent with public key 7xxxx use the 2.1 coins that it received to buy items from Amazon and later use the same 2.1 coins to buy more items from Walmart?

The bank checks that the agent hasn't already spent the coin that it is putting into a transaction.

Before permitting the transaction that double-spends the 2.1 coins with Walmart, the bank inspects the tamper-evident ledger for all transactions after transaction 3146 and before the Walmart transaction to ensure that the agent (7xxxx) hasn't already spent the 2.1 coins that it got in transaction 3146. The transaction that spends the coins at Amazon will show up in the ledger, and so the transaction with Walmart will not be allowed.

Every agent that has the bank's hash pointer to the end of the tamper-evident ledger can inspect the ledger to check that double-spending hasn't occurred.

The bank signs a valid transaction and appends it to the tamper-evident ledger. All agents can see the bank's signature and verify that nobody (not even the bank) has tampered with the tamper-evident ledger.

Example of a pay transaction

An example of the specification of a pay transaction is:

(9431, pay,
  [(3146, 0), (4731, 2)],
  [(0.7, 7xxxx...), (4.6, 9xxxx...)]
).

The id of this transaction is 9431; the type of the transaction is pay; the payers into the transaction are identified by the pairs of (transaction-id, index): (3146, 0), and (4731, 2); and the payee array is [(0.7, 7xxxx...), (4.6, 9xxxx...)].

Transaction validity

The bank appends a transaction to L if and only if the transaction is valid. The bank checks for validity by carrying out the following steps:

The bank verifies that the payers into the transaction signed the transaction.
The bank checks that the total value of coins paid out from the transaction does not exceed the total value paid in to the transaction. (If the value paid in exceeds the value paid out then the bank takes the difference as a transaction fee. More about fees later.)
The bank verifies that the payers' claims to have received coins in previous transactions is genuine. For example, if the agent with public key 7xxxx... claims to have received coins worth 2.1 in the transaction with id 10, and payee array index 0, then the bank verifies this claim by that transaction.
The bank ensures that coins paid into the transaction haven't already been spent.

Optimizations: Blocks and Block Chain

Verifying large numbers of small transactions requires more computation than verifying small numbers of blocks of many transactions. A block chain is a tamper-evident ledger in which each element of the ledger is a block consisting of many transactions. A block of transactions can be aggregated into a single large transaction by aggregating all the payers and payees of the smaller transactions.

The amount of computation decreases as the number of transactions in a block increases. The time required to fill a block with transactions is larger when the number of transactions to fill the block increases.

Checking the Trusted Agent

Consider a system in which the trusted agent broadcasts its current copy of the tamper-evident ledger to all agents. Every agent can inspect its copy of the tamper-evident ledger to determine whether the ledger has been tampered with. So, every agent can validate its trust in the trusted agent; however, this validation suffers from a crucial problem: Agents may only have copies of old, stale versions of the ledger. By the time that an agent receives a copy of the ledger, the trusted agent may have added more transactions to the ledger.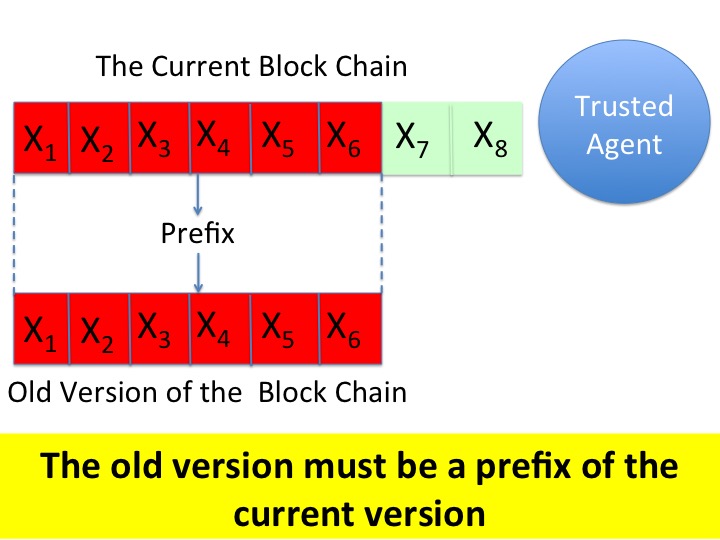

Fig4 — Fig.4: Old Copy is a Prefix of the Block Chain

An old copy of the ledger can differ from the current copy in only one way: the current copy may have transactions appended to the end of the old copy. So all agents can validate past behavior of the trusted agent. An agent cannot, however, treat its copy of the ledger as the master copy because the agent may not have the transactions added most recently to the ledger.

In the next module we will see how the Bitcoin algorithm addresses this problem.

Advantages of this cryptocurrency

Any agent can get a copy of the tamper-evident ledger and verify that all transactions in the ledger are valid. Any agent can verify that the only way in which the ledger is modified is that elements are append to its tail; all that the agent needs to do is to check that the pointer to the tail is modified only by appending elements. Because the ledger is tamper-evident, an agent can check that the ledger doesn't change while the hash pointer to the end of the ledger doesn't change.

The bank can't forge a transaction because all payers sign the transaction. Agents can remain anonymous because an agent's only public information is the agent's public key, and an agent can create multiple public keys. Every agent can verify the correctness of every transaction.

Disadvantages of this cryptocurrency

Users may not trust the bank. Transactions are not private because the bank has a record of all transactions. And the bank is a single point of failure.

Next we'll look at Bitcoin's algorithms for implementing a cryptocurrency without trusted agents.

Review

What is collision resistance? Why is it relevant to cryptocurrencies?
Consider the example of hiding in which Megan hides her predictions for the winner of the World Cup. Suppose you could choose two different random number generators for creating the secret \(r\); in one case the bits of \(r\) are uncorrelated, and in the other they are highly correlated. Which generator would you use and why?
What is binding? Why is it relevant to hiding information?
What is puzzle friendly?
What is a tamper-evident data structure? How would you implement a tamper-evident linear list? A tamper-evident tree?
Describe the algorithm for cryptocurrency with a trusted agent to someone who knows absolutely nothing about cryptocurrency.
How could the algorithm for cryptocurrency be used for a collection of distributed agents to keep track of a sequence of events, other than buying/selling currency?

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology