Byzantine Consensus: Written Messages

This module introduces Byzantine consensus algorithms in which agents reach consensus in a sequence of synchronized rounds even though some agents don't follow the protocol.

In this module we study algorithms by which a collection of agents reach a consensus among alternative values. The Paxos algorithm is an example of how agents reach consensus. Agents cannot reach consensus if message delays or agent operations are arbitrarily slow. Next, we study a consensus algorithm in which message delays are bounded and in which agents are guaranteed to come to a consensus even though some agents do not follow the protocol.

The algorithm operates in a sequence of steps called rounds. All messages sent in a round are delivered in the next round. Agents execute actions in each round after receiving messages sent in the previous round; these actions may include sending messages. So, the Byzantine algorithm is synchronous.

Byzantine Generals Problem: Overview

A general has \(N\) army units each of which is led by a lieutenant general, herafter referred to merely as lieutenant. We refer to the general and the lieutenants, collectively, as agents. An agent may be either loyal or disloyal. A loyal general gives the same command to all lieutenants. A loyal general's command is either attack or retreat. A disloyal general may give different commands to different lieutenants and may give no commands to some. The lieutenants receive commands from the general and then communicate among themselves to reach a consensus. Loyal lieutenants follow an algorithm while disloyal lieutenants may or may not.

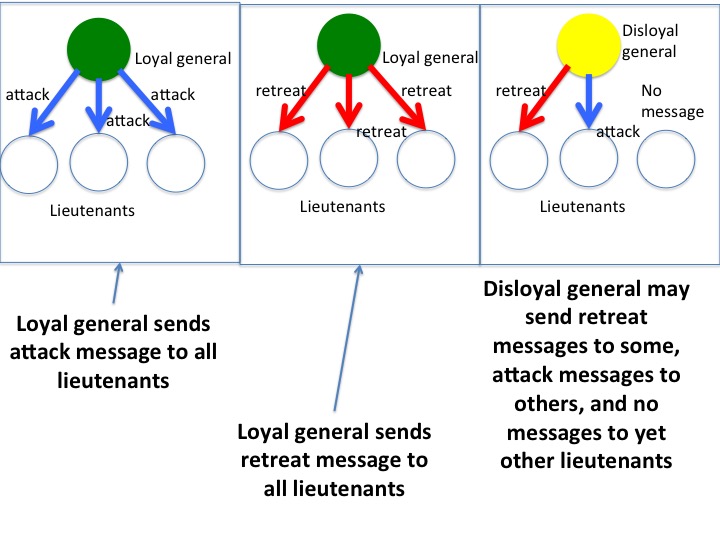
The figure below illustrates the difference between loyal and disloyal generals.

Byzantine Generals Problem: Specification

A loyal general sends attack messages to all lieutenants or sends retreat messages to all lieutenants. A disloyal general sends arbitrary messages to lieutenants.

1. Validity: Loyal lieutenants must obey a loyal general. If a loyal general gives the command to attack then all loyal lieutenants must attack. Likewise, if a loyal general gives the command to retreat then all loyal lieutenants must retreat.
2. Consensus: Loyal lieutenants come to a consensus: either all of them attack or all of them retreat.

The specification does not require that traitors be discovered. For example, the algorithm doesn't have to determine whether the general or a lieutenant is loyal or disloyal.

If the only requirement is validity, and consensus isn't required, then the solution is trivial: all loyal lieutenants obey the general whether the general is loyal or disloyal. If the only requirement is consensus then the solution is trivial: all loyal lieutenants agree on a predefined value, say retreat, regardless of the command issued by the general. The conjunction of both requirements makes the problem difficult.

Oral and Written Messages

There are two versions of the problem.

1. Written Messages: In this version an agent may send copies of messages that it receives to other agents but cannot modify the messages. Also, an agent cannot forge signatures. So, an agent can receive a message M signed by lieutenant \(A\) only if \(A\) sent M to some agent.
2. Oral Messages: In this version an agent can modify messages and forge signatures.So, an agent can receive a message M signed by agent \(A\) even if \(A\) never sent M to any agent.

The algorithm for written messages is simpler and requires fewer messages.

Algorithm with Written Messages

A reliable lieutenant who does not get a message from in round 0 treats the absence of the message as the same as receiving a retreat message. Likewise, if a loyal lieutenant gets a message that is not an attack or a retreat message then the lieutenant treats the message as a retreat message. (We use retreat as a default. We could just as well have used attack as the default.)

Next, we give an overview of the algorithm.

Commit to Attack

At each round in the algorithm, a loyal lieutenant has either committed to attack or not. A lieutenant that has not committed to attack on a round may commit to attack on a later round. If any loyal lieutenant commits to attack in any round then it remains committed to attack thereafter. A loyal lieutenant retreats if it has not committed to attack at the end of the last round.

Messages

A message is an attack message from the general or a commitment to attack by a lieutenant. We call commitment messages attack messages. An attack message is identified by the agent (general or lieutenant) that created the message.

Evidence for Attack

A loyal lieutenant commits to attack on round \(r \geq 1 \), for the first time, if the lieutenant has received an attack message from the general and at least \(r - 1\) lieutenants. When the lieutenant commits to attack it sends copies of these messages, and its own attack message, to all other lieutenants. So, in round \(r+1\), each lieutenant receives an attack messages from the general and at least \(r\) lieutenants. And so, all loyal lieutenants commit to attack in this round.

The Algorithm

We will use the tactic that is helpful in analyzing distributed algorithms that operate in rounds. We will prove properties of a sequential algorithm and then show the equivalence of the sequential and distributed algorithms. The sequential algorithm is given next.

Local Variables

Associated with each lieutenant C are local variables C.received and C.sent which are sets of agents (general or lieutenants). C.received is the set of agents from which C has received attack messages (or their copies). C sends attack messages (or copies) from agents in C.sent. The symbol g represents the general.

Initialization: Round 0

A.sent = {} for all lieutenants A.

1. If the general is loyal and sends attack messages then the set of agents from which a lieutenant has received attack messages is the singleton set consisting of the general. So, for all lieutenants A:
   A.received = {g}
2. If the general is loyal and sends retreat messages then for all lieutenants A:
   A.received = {}
3. If the general is disloyal, then A.received = {g} for some lieutenants A, and A.received = {} for the others.

The algorithm operates in a sequence of rounds with round-number r stepping from 1 to t+1. The r-th iteration for loyal agent c consists of the following two steps.

Round r > 0

Step 1

if (|C.received| >= r) AND  (g in C.received):
    C.commit = True
    C.sent = C.received UNION {C}

If C.received has messages that show that: (1) the number of agents that have committed to attack on round r is at least r, and (2) the general has sent an attack message, then C commits to attack and sends these messages as well as an additional message that C has committed to attack.

Step 2

C.received = (
    (UNION over all loyal agents B of B.sent)
             UNION
     an arbitrary subset of disloyal agents)

C receives the messages sent by loyal lieutenants and messages sent by disloyal lieutenants. A disloyal lieutenant, A, can send messages to some lieutenants that A is committed to attack, and not send these messages to other lieutenants. Lieutenant C receives attack messages from an arbitrary subset of disloyal lieutenants.

Lieutenant C does not know which agents are loyal and which are disloyal. C.received is the set of all messages sent to C regardless of whether the senders are loyal or disloyal.

Proof of Correctness

Case 1: General is loyal and sends attack messages

In this case, at the start round 1, C.received = {g}. So, the if-clause in step 1 of round 1 is True, and therefore all loyal lieutenants commit to attack at the end of round 1.

Case 2: General is loyal and sends retreat messages

A disloyal lieutenant cannot forge the general's signature, and so it is impossible for any lieutenant to have a copy of an attack message from the general. Therefore the if-clause of step 1 is never satisfied, and so no loyal lieutenant commits to attack in any step.

Case 3: General is disloyal

Part 1

We first show that if any loyal lieutenant commits on round r then all loyal lieutenants commit by the end of round r+1.

A loyal lieutenant C commits on round r exactly when the set C.received has at least r attack messages including one from the general. So, in round r, C.sent has at least r+1 attack messages including one from the general. Therefore, the if-clause of step 1 evaluates to True in round r+1, and so all loyal lieutenants commit by the end of round r+1.

Therefore, if any loyal lieutenant commits by the end of round t-1 then all loyal lieutenants commit by the end of round t.

Part 2

We next show that if no loyal lieutenant has committed by the end of round t-1 then no loyal lieutenant commits in round t.

C.sent = {} at the end of round t-1 if no loyal lieutenant has committed to attack. Therefore in round t, C.received is an arbitrary subset of disloyal lieutenants. There are at most t-1 disloyal lieutenants because there are at most t disloyal agents, and the general is disloyal. So, on round t, the if-clause of step 1 evaluates to False.

Part 3

From parts 1 and 2, by the end of round t, either all loyal lieutenants commit, or no loyal lieutenant commits.

Example

The figure below illustrates a situation in which a loyal lieutenant C commits to attack on round 3, if it hasn't already committed to attack on rounds 1 and 2. The figure shows C getting attack messages (red boxes) signed by the general and lieutenants A and B on round 2. The general and lieutenants A and B may be disloyal or loyal.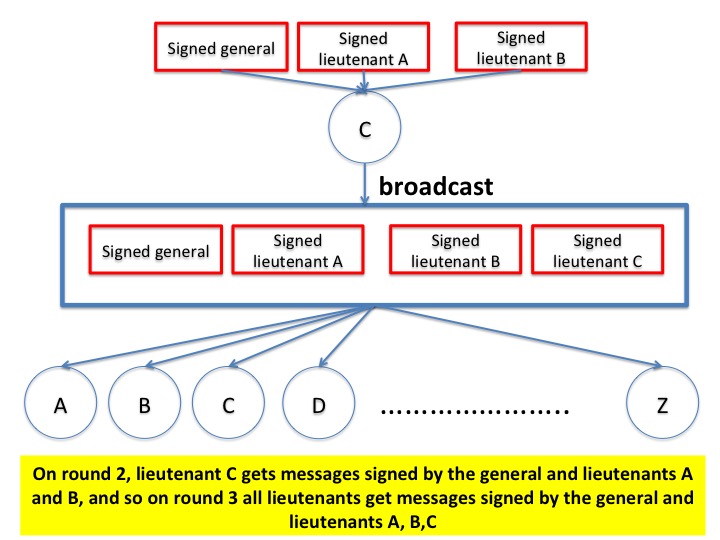

Because C is loyal it follows the algorithm, and C commits to attack at the end of round 3 because C receives a signed attack message from the general and signed attack messages from two different lieutenants. So, in round 3, C broadcasts copies of attack messages signed by the general and attack messages signed by A and B and attack messages, and also an attack message signed by C itself. All loyal lieutenants commit to attack in round 4 because they receive attack messages signed by the general and 3 different lieutenants (A, B, C).

Review

1. Assume that you are explaining the algorithm to someone who hasn't taken a course on distributed computing. How would you explain to this person that even if the general and 999 lieutenants are disloyal, and only 2 lieutenants are loyal, the loyal lieutenants reach a consensus after round 100? (Remember the first round is round 0.)
2. Will the algorithm work if at most one lieutenant could modify written messages, and all the other lieutenants followed the protocol, i.e. these lieutenants could copy but not modify messages.