Consensus Algorithms
This page outlines the idea behind the proof that consensus is impossible in distributed systems that may have faulty agents and in which message delays are arbitrary.
Importance of Consensus Algorithms
Algorithms by which groups of agents come to a consensus are among the most fundamental in distributed computing.
There are many problems in which messages are sent to groups of agents who collectively maintain a common consensus state. Multiple agents reduce the possibility of system-wide failure due to the failure of a single agent. For example, a bank may use a group of agents, rather than a single agent, to maintain bank balances.
Managing replicated databases requires the replications to come to a consensus on the sequence of transactions that is applied to the database. Cryptocurrency transactions require agents to come to a consensus about sequences of transactions that use crypto coins.
In a control system with multiple and actuators, the actuators have to come to a consensus about the state of the environment so that they can operate in concert. A vehicle would crash if some actuators caused the vehicle to accelerate while other actuators applied brakes. In some applications, multiple agents have to come to a consensus to elect a single leader. There are many problems in which agents have to reach a consensus.
Consensus: Impossible with a faulty agent
Consensus is impossible with even a single faulty agent. This was proved by Fischer, Lynch and Patterson.You can get the idea of why consensus is not possible by considering the following problem in which message delays are finite but arbitrarily long, and in which agents may fail by halting forever.
A collection of 2N + 1 agents want to come to a consensus about a color. N of the agents pick blue and N+1 pick red. One of the red agents is arbitrarily slow. The 2N non-slow agents exchange messages among each other, and each of these 2N agents gets N votes for red and N votes for blue. Agents decide to take a majority vote, and in the event of a tie pick blue.
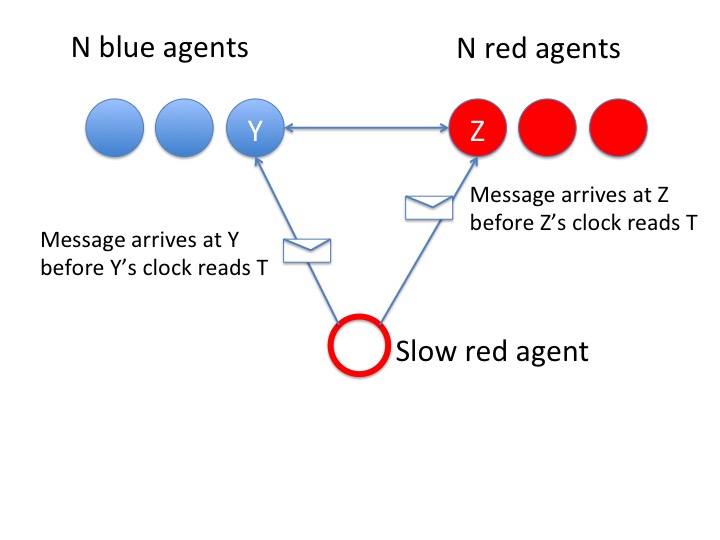
How long should they wait for the slow agent?
Consider an algorithm in which agent waits until its local clock shows an elapsed time of T and then makes a decision based on the votes that it has. An agent Y gets N red and N blue votes when its clock shows an elapsed time of T, and agent Y decides that the consensus is blue. Another agent Z has a slower clock and gets a red vote from the slow agent for a total of N+1 red votes, before Z's clock shows an elapsed time of T. So Z determines that the consensus is red. The algorithm fails because Y and Z have not come to a consensus.
No algorithm is guaranteed to come to a consensus in finite time if messages or agents can be arbitrarily slow because algorithms cannot distinguish between slow agents and agents that have halted. Systems with synchronized clocks don't have this problem. Later, we'll look at consensus algorithms for systems in which agents operate in synchronized rounds.
Best Effort Consensus
The theorem says that there is no algorithm that guarentees that consensus can be reached in all scenarios; however, consensus can be reached in most practical situations.
An idea to overcome the problem identified in the counterexample given above is as follows: Agents keep trying repeatedly until they reach consensus. The theorem tells us that the agents may have to keep trying for ever. We expect, however, that in most practical situations their attempts will succeed at some point. A "best effort" algorithm may not terminate; but, if it does terminate then it terminates in a state in which the collection of agents have reached a consensus.
What does "keep trying" mean? When does one trial end and the next one begin? If agents use timeouts to end a trial, then --- because clocks aren't synchronized --- the timeouts may complete at different times. In the next pages we will see that we can use the idea of time, even though clocks aren't synchronized, to design a best-effort consensus algorithm.
Next
Next we see how ideas similar to logical times, can be used to serialize transactions in faulty systems.Serializability plays a key role in the development of the consensus algorithm, Paxos. Later, we will study Byzantine consensus and consensus using block chain.
K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology