Progress

We show that a distributed system progresses towards its goals by using variant functions, just as we do to prove that while loops terminate execution. Later, we discuss temporal logics that provide a theory for reasoning about temporal properties of computations.

Why a Temporal Logic is Necessary

The following diagram illustrates why temporal logic is necessary.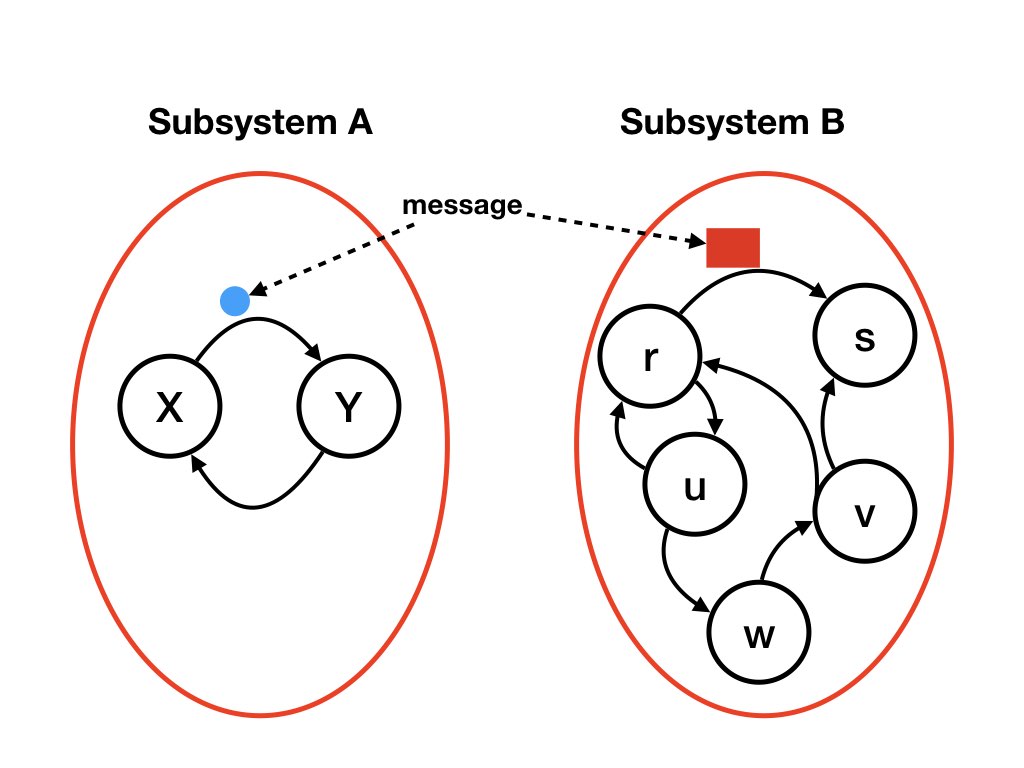

The diagram shows a system consisting of two subsystems A and B. Subsystem A consists of two agents X and Y that exchange a token -- they sending the token back and forth for ever. When the token is in channel (X, Y), agent Y puts the token on channel (Y, X). Likewise, when the token is in channel (Y, X), agent X puts the token on channel (X, Y).

The agents and channels in subsystem B don't matter for this illustration. The state shown in the diagram has a message in the channel (X, Y) and a message in channel (r, s).

Let's look at the while loop that generates computations of the system.

while there exists a nonempty input channel in the system:
   select a nonempty channel (u, v) in the system
   let the head of channel (u, v) be msg
   v executes receive(msg, u)
  

There are many executions of the loop depending on which nonempty channel is selected. One of the many possible executions of the loop is as follows. Forever select channel (X, Y) and then (Y, X).

In this execution the message in channel (r, s) remains in the channel forever. To prove properties of the entire system we must represent steps taken by subsystem B as well.

One way to deal with this problem is to extend variant functions as described in the following paragraphs. The idea is to require that if there is a nonempty channel (r, s) then that channel will be selected eventually.

By eventually we mean in a finite number of iterations of the while loop. We don't have an upper bound on the number of iterations before nonempty channel (r, s) is selected, but it will be selected. Temporal logics allow us to reason about eventuality. Later we will describe temporal logics CTL, LTL, and UNITY.

Progress in a Distributed System

In some cases, distributed algorithms are designed not to terminate. In such cases we typically need to show that if a predicate P holds in some state of a computation then a predicate Q holds then or later. For example, if an agent is waiting to acquire access to a file then it will eventually get access to the file.

We extend the proof of loop variants for this purpose. We introduce the relation leads_to between predicates where P leads_to Q, also written as P \(\leadsto\) Q, means that if P holds after n steps in a computation then Q holds at after n' steps in the computation where \(n' \geq n\). We don't know \(n' - n\) but we know that it is finite.

Let f be a function from the states of the system to a well-founded set (exactly the same as a loop variant). We prove P leads_to Q by showing the following properties called the safety and progress properties of the loop variant.

If P and (f <= k) and not Q
holds before an execution of the loop body then:

1. Safety: For any nonempty channel (u, v) after a message is received on the channel the following holds:
   (P and (f <= k)) or Q
2. Progress: There exists a nonempty channel (u, v) such that after a message is received on the channel the following holds:
   (P and (f < k)) or Q

The safety property, without the progress property, allows for the possibility that

P and (f = k) and not Q remains true for ever. The progress property disallows that possibility. Why? Because the nonempty channel (u, v) will be selected eventually. The post-condition after the message on channel (u, v) is processed is (P and (f < k)) or Q. So, (P and (f = k)) or Q does not hold forever. The remainder of this page consists of examples.

Examples

Example: greatest common divisor across a network

Consider the example given in the page on invariants: find the gcd of the local variables of agents in a strongly connected network. The receive function is given again for convenience.

def receive(message, sender):
   if n != gcd(n, message):
      n = gcd(n, message)
      for successor in successors:
         send(n, successor)

The problem is to prove that the algorithm terminates. A proof that the algorithm terminates is based on the following loop variant: (N, M) where N is the sum of X.n over all agents X and M is the total number of messages in channels. Comparisions of tuples are made lexicographically:
(i, j) < (x, y) exactly when (i < x) or ((i = x) and (j < y)).

We prove that execution of each receive reduces (N, M). Consider two outcomes of the if statement:

1. If n is different from gcd(n, message) then n decreases and therefore N decreases.
2. If n = gcd(n, message) then a message is removed and no messages are sent; this reduces M while leaving N unchanged, and so the loop variant decreases.

.

Example: Eventual Consistency

A network of agents consists of a single master database and satellite databases. Each satellite database contains copies, possibly out of synch, with the master. There is a path in the network from the master to all satellites. The master is the only database that is modified.

When the master is modified it assigns a higher version number to the new value and sends copies of the new value on its output channels. When a satellite gets a copy on its input channel, if the version is later than the satellite's copy then the satellite updates its copy and sends the new value on its output channels. The system is initialized with all agents at version number 0.

Let A be the master. Let x.n be the version number of the copy at a agent x. An invariant I of the system is:
for all x: x.n \(\leq \) A.n

The problem is to show that if the master version number is some value N or greater then all the satellite versions catch up to N. We prove that P leads to Q where
P is A.n \(\geq\) N
Q is for all x: x.n \(\geq\) N

A loop variant f is the number of satellites whose copies have version number less than N. The loop variant is bounded below. The proof of the safety property of the loop variant is straightforward.

The proof of the progress property is as follows. If P and not Q holds then there is a channel (y, z) where y.n \(\geq\) N and z.n \(<\) N. From invariant Inv_2 there is a message in the channel. After the message in the channel is received z.n \(\geq\) N, and so f is reduced.

---

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology