Loop Termination: Variant Functions
This module is a review of methods used to prove that executions of loops terminate.
We will prove that executions of loops terminate by using loop variants. We also use the term variant function for loop variant. We will use variant functions to prove termination of distributed systems.A variant function is a function from states of a system to a well-founded set. A well-founded set is a set on which we can carry out proofs by induction. In this course we generally use well-founded sets that are integers or vectors of integers, and that are bounded below. We compare vectors lexicographically. For example \((0, 2) < (1, 0)\).
Let \(f\) be a variant function. Then \(f = k\), for a constant \(k\) is a predicate. The extension of this predicate is the set of states \(s\) where \(f(s) = k\).
We prove that execution of a loop terminates by proving that the execution of any command whose guard evaluates to True reduces the value of a variant function \(f\).
If the execution of any command with a True guard reduces \(f\) then every iteration reduces \(f\). Since \(f\) is bounded below, it cannot decrease forever. Therefore, the computation terminates.
Variant Functions and Hoare Triples
Let \(I\) be an invariant of the loop, let the \(j\)-th guarded command have guard \(g_{j}\) and command \(c_{j}\), and let \(f\) be a variant function of the loop. We prove that the execution of any command with a True guard reduces the variant function by proving the following Hoare triple for all \(j\):\(\forall K: \quad \{(f = k) \wedge I \wedge g_{j}\} \; c_{j} \; \{f < k\} \)
Because \(I\) is an invariant it holds before every command is executed. Since \(c_{j}\) is executed only if \(g_{j}\) holds, we know that \(I \wedge g_{j}\) holds before \(c_{j}\) is executed. Execution of the command reduces the variant function from \(k\) to some smaller value.
Variant Functions and Graphs
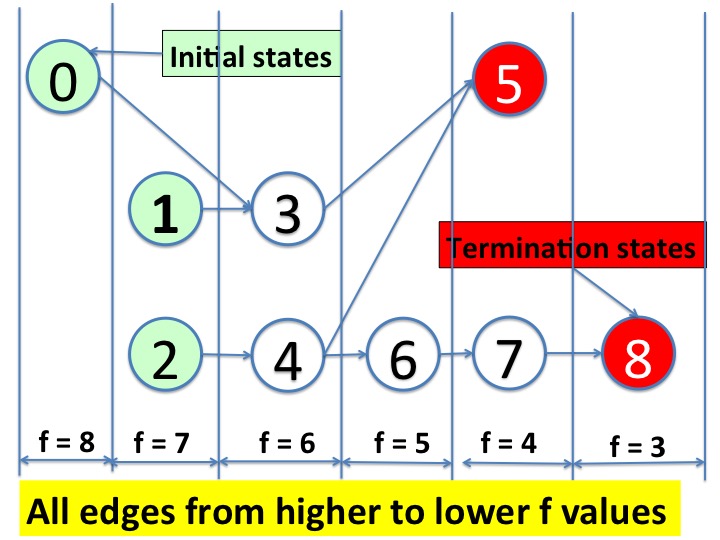
If an algorithm has a variant function \(f\) then all paths in from initial vertices are cycle-free. This is because every edge on the path is from a state with a higher value of \(f\) to a state with a lower value. The diagram below shows an acyclic graph with edges directed from higher to lower \(f\) values.
A terminal state (vertex) is one without outgoing edges.
The existence of a variant function tells us that a terminal state is
reached from an initial state in a finite number of state transitions.
 >
>
Self tests
are given in Examples of Correctness Proofs.Review
- What is a variant function? What does lexicographical comparison of vectors of integers mean?
- Can a loop that executes forever have a variant function? Why not?
K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology