Distributed Algorithms Contents Index

Invariant and Stable Predicates

This module reviews invariant and stable predicates in nondeterministic loops.

Stable

A predicate \(P\) on states is stable exactly when all transitions from states in which \(P\) holds are to states in which \(P\) holds.

In the state-transition diagram, a set \(P\) of vertices is stable exactly when all edges from vertices in \(P\) are to vertices in \(P\). Because there are no transitions from inside a stable set to outside the set, there are also no paths from states inside a stable set to states outside the set. There may, however, be paths from outside a stable set into the set.

Fig1>
Fig.1 - Paths from a stable set remain in the set

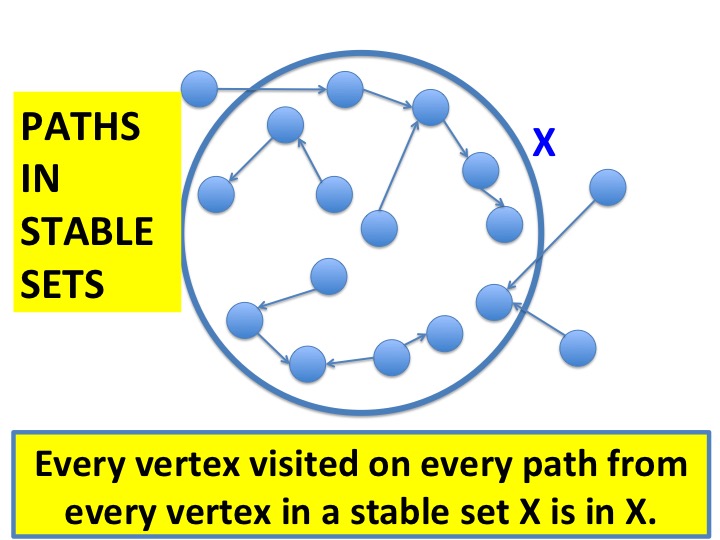We prove that a predicate \(P\) is stable for a do-od loop by showing that it is maintained by all its guarded commands:

\( \{P\} \; g \rightarrow c \; \{P\} \)

Initial Conditions and Invariants

The initial condition of a loop is a predicate that holds when iterations of the loop are initiated; let's call this predicate \(init\). An initial state of the system is any state for which \(init\) holds. We assume that a computation starts in some state, i.e. we assume that there exists at least one state in which \(init\) holds.
An invariant of a do-od loop is a stable predicate that holds initially.

Safety Proof Obligation

Let \(safe\) be a set of states where we want to prove that all paths that start in states in \(init\) remain in \(safe\). Our safety proof obligation is to show that every state on every path from every state in \(init\) is in \(safe\).

We prove safety by finding a stable vertex set \(I\) such that:

\( init \subseteq I \subseteq safe \quad \)

Fig2>
Fig.2 - Illustration of Invariant I

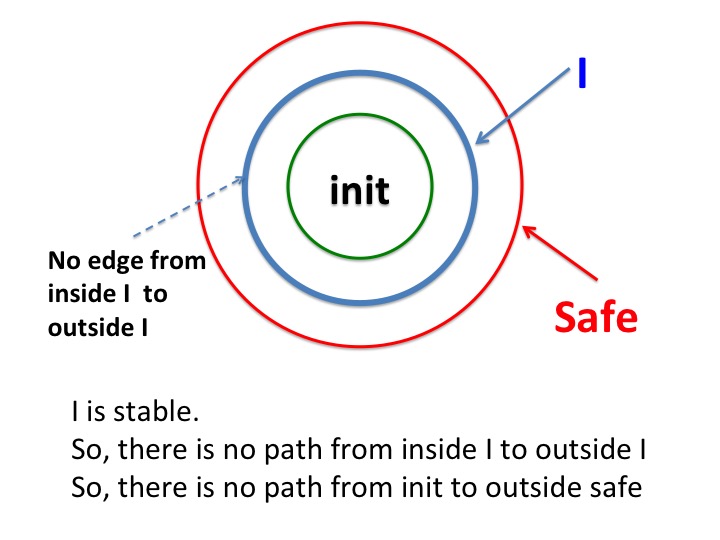Because \(I\) is stable, all paths from \(I\) remain within \(I\). Because \(init\) is a subset of \(I\), all paths from \(init\) remain within \(I\). All paths from \(init\) remain within \(safe\) because \(I\) is in \(safe\).

The initial condition and invariant specify an initial and invariant set of states in the state-transition diagram. All paths from initial states remain forever in the invariant set of set of states.

Self tests

are given in Examples of Correctness Proofs.

Summary

Proofs of safety for distributed and sequential algorithms are identical. We will review the material in this module when we discuss safety.

Review

  1. What is a stable predicate? What is an invariant?
  2. How can you prove that all paths from an initial set of states remain in a given set, safe, of states?

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology