Self Test: Flight Formation

This self test is to prove a concurrent system in which a collection of agents in space, move towards a formation, even though each agent can only communicate with its neighbors.

Specification

Agents \(0\) and \(N\) are called anchors. The anchors are stationary while the other agents move so as to create a specified formation. For \(0 < j < N\), agent \(j\)'s neighbors are agents \(j-1\) and \(j+1\).

Let agent \(j\)'s location be \(l[j]\), and let its initial value be \(l[j]^{0}\). When the computation terminates, the anchors must be at their initial positions, and the locations of other agents must be \(\epsilon\)-close to the midpoint of the locations of its neighbors.

1. Anchors are stationary.

   \( (l[0] = l[0]^{0}) \wedge (l[N] = l[N]^{0}) \)

2. Other agents are approximately at midpoints of their neighbors. \( \forall 0 < j < N : \) \( \quad |l[j] - mid | < \epsilon \)

   where \(mid = (l[j-1]+ l[j+1])/2 \)

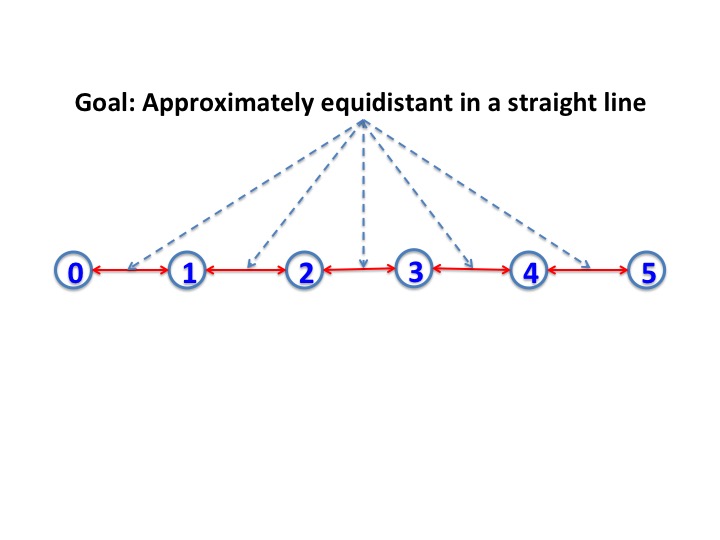
The figure below shows the desired terminal state.

>

Agent Actions

Agents \(0\) and \(N\) are stationary. The action of agent \(j\) for \(0 < j < N\) is as follows. If the distance from the agent's location to the midpoint of its neighbors is more than or equal to \(\epsilon\) then the agent moves to the midpoint; otherwise, the agent does nothing.

The action is specified by the following program segment. Let \(l\) be the vector of agents' locations where \(l[j]\) is the location of the \(j\)-th agent.

    mid = (l[j-1] + l[j+1])/2.0
    if |l[j] - mid| >= epsilon:
         l[j] = mid
    

The program segment is equivalent to the guarded command:

\( |l[j] - mid| \geq \epsilon \quad \rightarrow \quad l[j] = mid \)

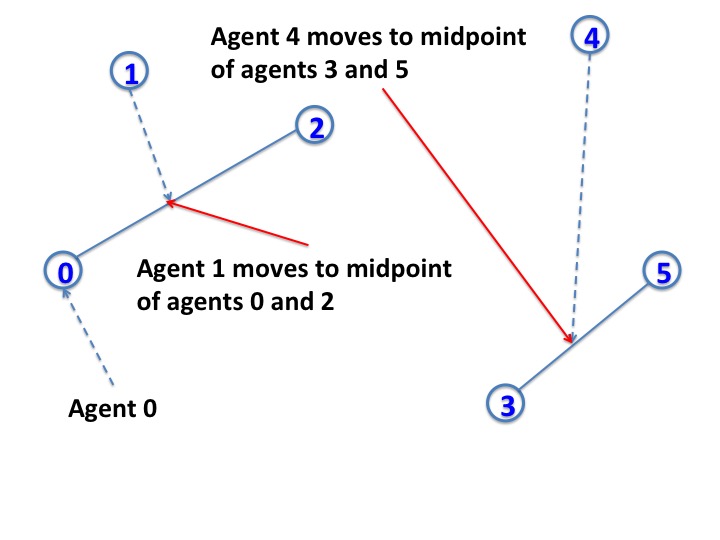
The figure below shows an example with agents indexed 0 through 5. The figure shows the movement of agent 1 to the midpoint of agents 0 and 2. The figure also shows the movement of agent 4 to the midpoint of agents 3 and 5. All the agents can move simultaneously; however, for simplicity we will assume that only one agent moves at a time.

>

The next figure shows 3 diagrams from top to bottom. The diagram at the top is the state at some point. The diagram in the middle shows the state after agent 1 (red) moves to the midpoint of agents 0 and 2. The diagram at the bottom shows the state after agent 3 moves to the midpoint of agents 2 and 4. Note that the agents seem to be moving away from the goal of having all agents on the line connecting the stationary agents 0 and 5.

>

Self Test: Proof of Correctness

Test 1

Give and prove an invariant of the loop.

Test 2

Prove that the loop terminates by giving a variant function for the loop.

Test 3

Show that the specification holds upon termination of the loop.

Answers

Answer 1

The invariant is: The anchors are stationary.

\( (l[0] = l[0]^{0}) \wedge (l[N] = l[N]^{0}) \)

Answer 2

A variant function \(f\) is the sum of the square of the lengths between neighboring agents.

\( f(l) = \sum_{j=1}^{N} ((x_{j} - x_{j-1})^{2} + (y_{j} - y_{j-1})^{2}) \)

This variant function is bounded below. You can show that the execution of any guarded command with a True guard reduces the value of the variant function by at least a positive constant \(\delta\). So, variant function value can decrease for only a finite number of steps.

We leave it to you to determine \(\delta\). The largest value of \(\delta\) is immaterial; all you need to do is show that there exists a positive value. (Hint: \(\delta\) depends on \(\epsilon\) and the initial configuration.)

Answer 3

We must show that if the invariant holds and all guards are false then the specification is satisfied. This is trivial.

Extensions

Design a similar algorithm in which agents move in 3-D space.

---

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology