Computation: Examples

Examples of computations:

1. Simple examples of balloons tossed between two children.
2. Example from previous pages.

Examples of invariants, loop variants, and termination condition:

1. Balloon example.
2. Distributed Greatest Common Divisor.

A Simple Example: Tossing Balloons (continued)

This example is a continuation from the example in States. Two children, X and Y, are tossing balloons to each other. A balloon that has been tossed by X, while in the air to Y, is a message in the channel (X, Y\). When a child gets a balloon it tosses the balloon back immediately. Initially there is a balloon tossed by X on its way to Y and there is also a balloon tossed by Y on its way to X.

Each child has a countdown of the number of times it tosses balloons. Each time a child tosses a balloon it decrements its countdown value. After a child's countdown reaches 0 the child pops balloons that it receives (and doesn't toss popped balloons).

Question

How is a state of this system specified?

Answer

The state of a channel is the number of balloons in it. The state of an agent (X or Y) is the countdown value nX or nY, respectively. The state of the system is given by the states of its agents and channels.

Question

What is an example of a computation of the system?

Answer

An example of a computation is shown in the diagrams below where the computation is State 1 to State 2 to .. State 6.

A Computation shown as a Sequence of Diagrams

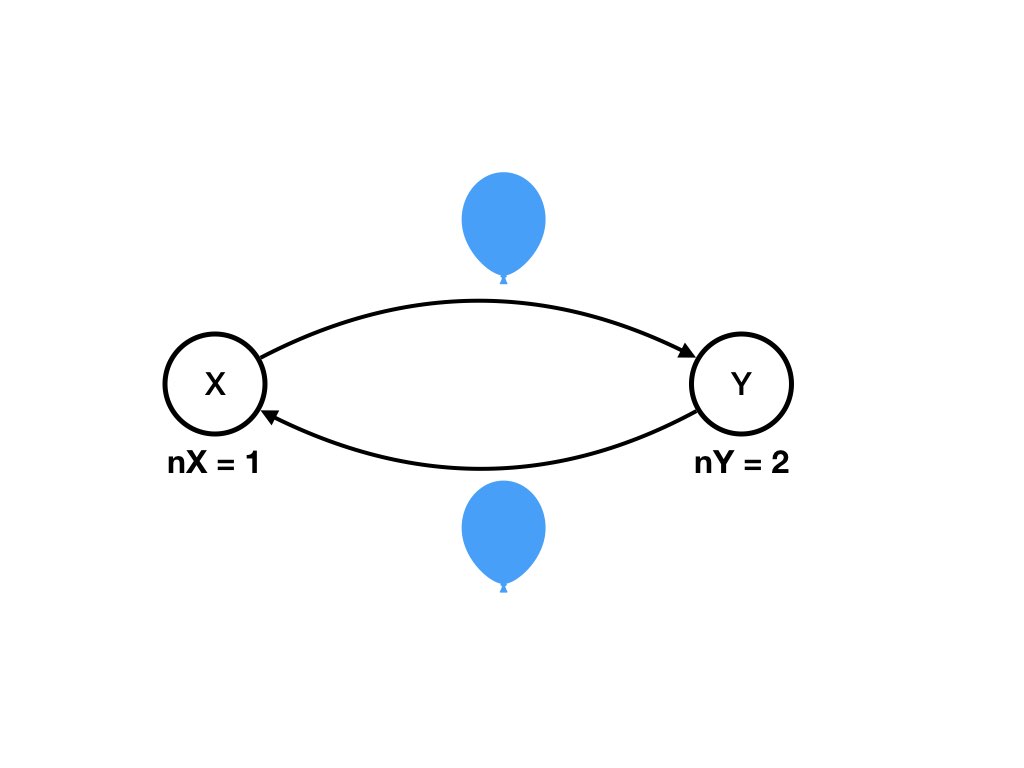
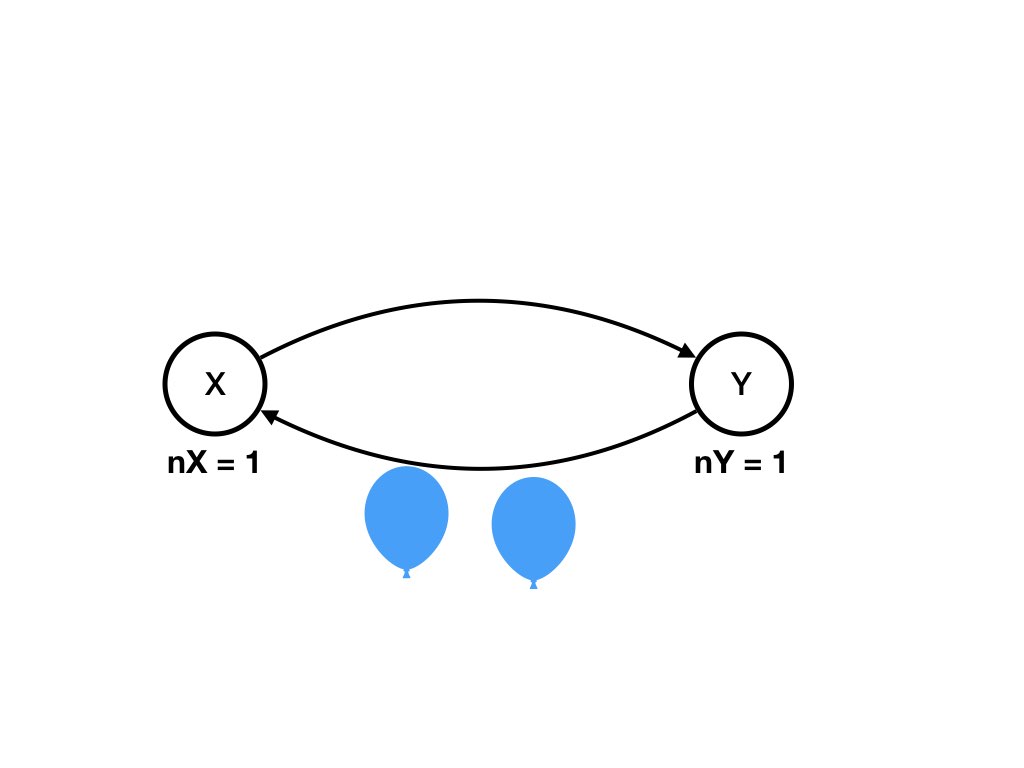
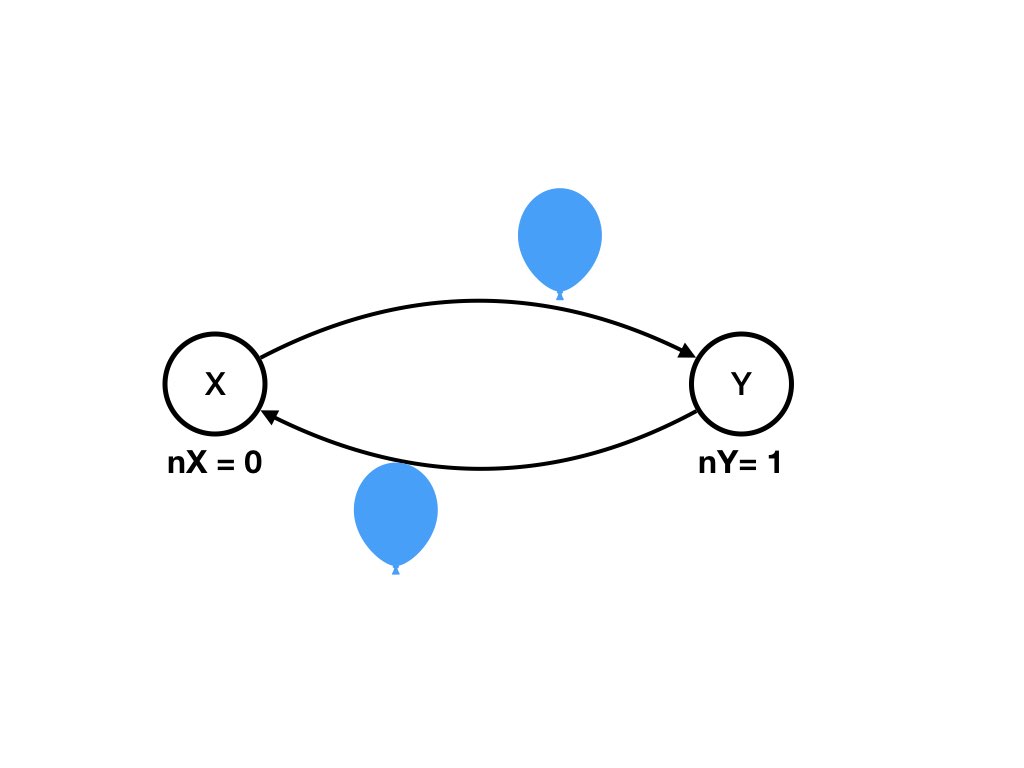
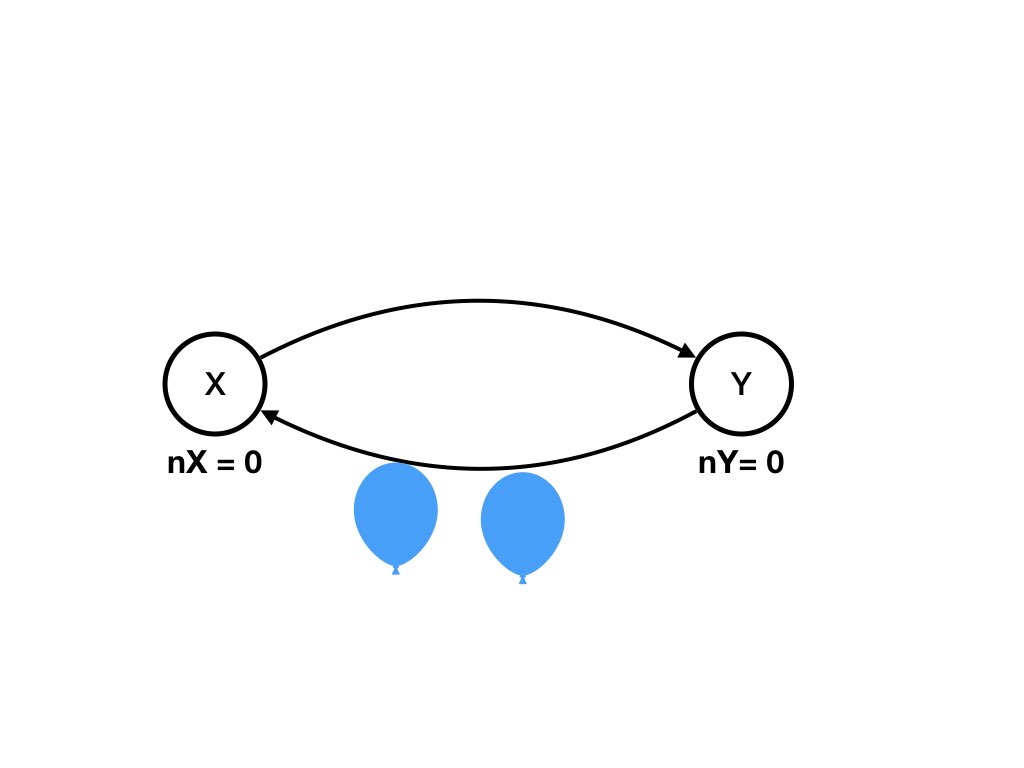
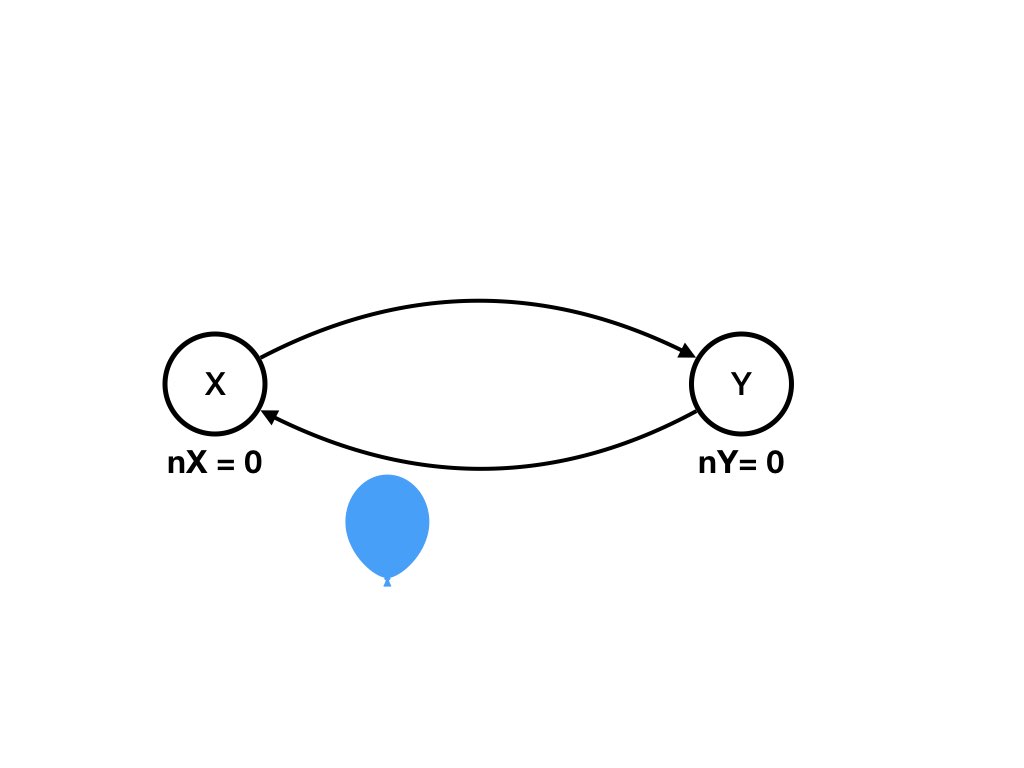
Question

Specify the computation which is shown above as a sequence of diagrams as a sequence of states.

Answer

The sequence of states, shown below, is the computation shown in the diagrams above. You can verify that there exists a transition from each state in the sequence to the next. Also see that each transition is caused by exactly one agent receiving exactly one message on one of the agent's input channels.

Initial State: Channel (X, Y) has one balloon and channel (Y, X) has one balloon. And the countdown for X is 2 and the countdown for Y is 3. We represent this state by:
nX = 1, nY = 2, (X, Y) = 1, (Y, X) = 1

The sequence of steps from the initial state are as follows.

1. Y receives a balloon and sends it back. So the state becomes:
   nX = 1, nY = 1, (X, Y) = 0, (Y, X) = 2
2. X receives a balloon and sends it back. So the state becomes
   nX = 0, nY = 1, (X, Y) = 1, (Y, X) = 1
3. Y receives a balloon and sends it back. So the state becomes
   nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 2
4. X receives a balloon and pops it. So the state becomes
   nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 1
5. X receives a balloon and pops it. So the state becomes
   nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 0

There are no further steps in this computation.

Question

What are other transitions from the initial state of the computation?

Answer

Let's look at the event in step 2 of the above computation. The event is as follows.

Event: X receives a balloon for the first time

This event is specified by the 4-tuple:

1. X's state before the event is nX = 1
2. The message that is received is 1 (balloon) and the message is from Y.
3. X's state after the event is nX = 0
4. The message that is sent in the event is 1 (balloon) and the message is to Y.

This event can be executed in any state S which satisfies the inputs to this event:

1. X's state before the event is nX = 1
2. The message at the head of channel (Y, X) is 1.

So, this event can be executed in the initial state.

The execution of this event causes a transition from the initial state to a state shown in the following diagram:

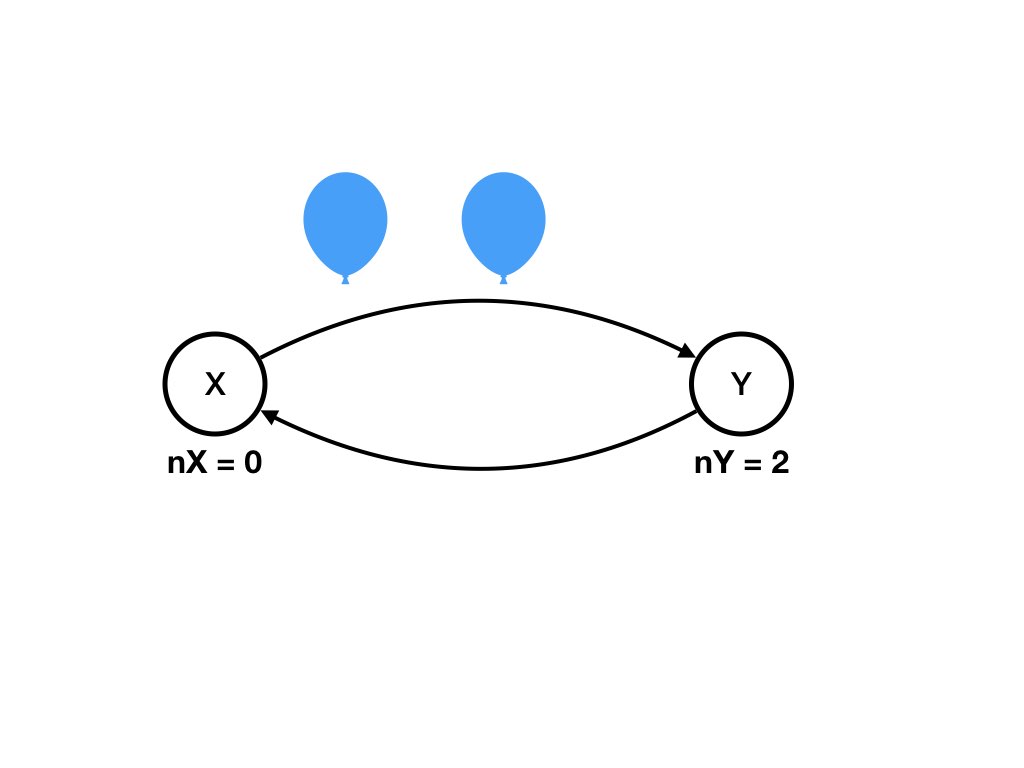
Question

Can you give examples of other computations starting in the same state?

Answer

Initial State: Channel (X, Y) has one balloon and channel (Y, X) has one balloon. And the countdown for X is 2 and the countdown for Y is 3. We represent this state by:
nX = 1, nY = 2, (X, Y) = 1, (Y, X) = 1

1. X receives a balloon and sends it back. So the state becomes:
   nX = 0, nY = 2, (X, Y) = 2, (Y, X) = 0
2. Y receives a balloon and sends it back. So the state becomes
   nX = 0, nY = 1, (X, Y) = 1, (Y, X) = 1
3. X receives a balloon and pops it. So the state becomes
   nX = 0, nY = 1, (X, Y) = 1, (Y, X) = 0
4. Y receives a balloon sends it back. So the state becomes
   nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 1
5. X receives a balloon and pops it. So the state becomes
   nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 0

There are no further steps in this computation.

Some states (e.g. State 2) in the first example of a computation don't occur in the second example, and vice versa.

A Computation of the System from Previous Pages

Question

What is an example of a computation, starting from the initial state, of the example?

Answer

The following sequence of diagrams shows a computation of the example. Each diagram shows a state of the system. There is a transition from state S_k to state S_(k+1)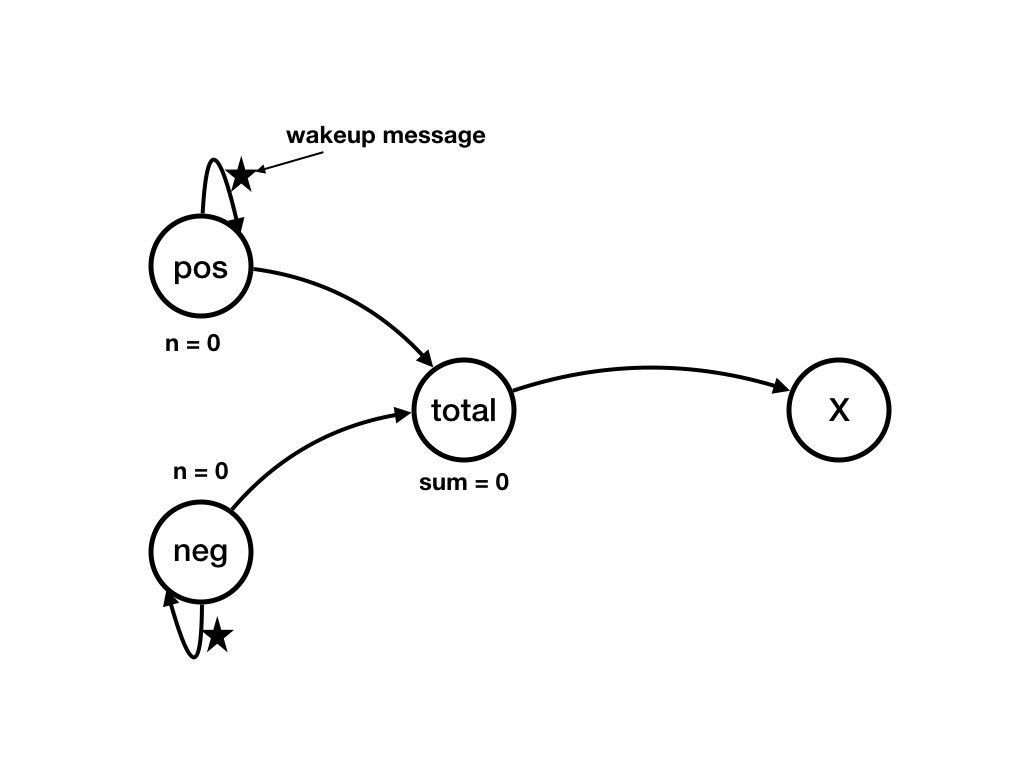

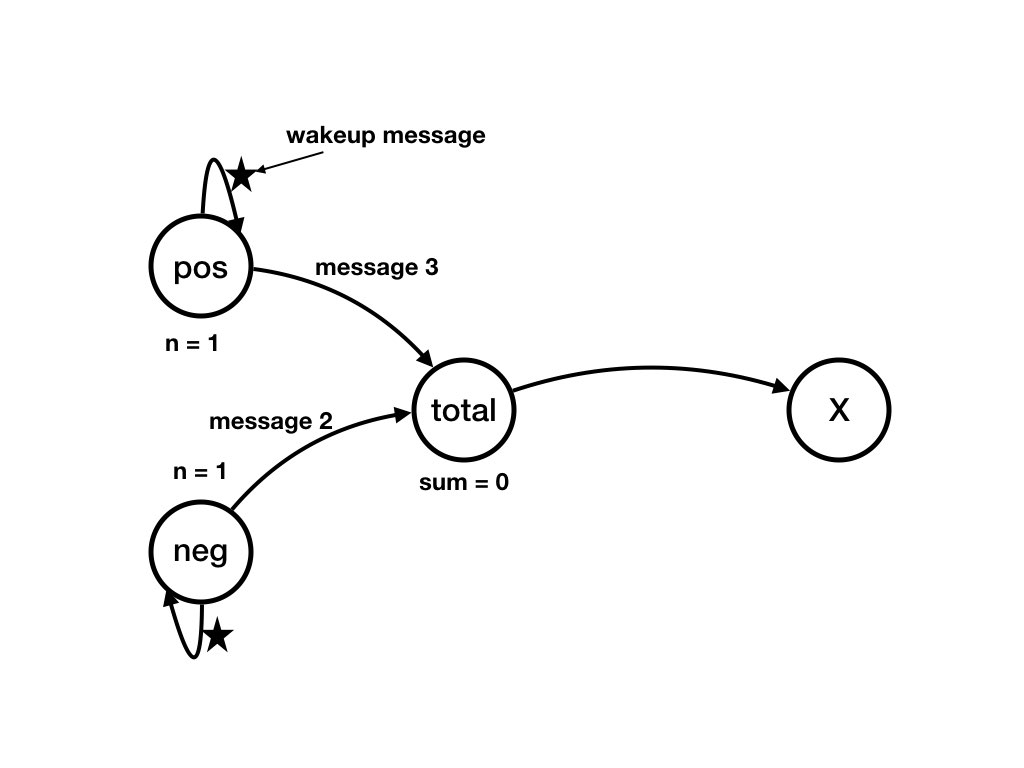
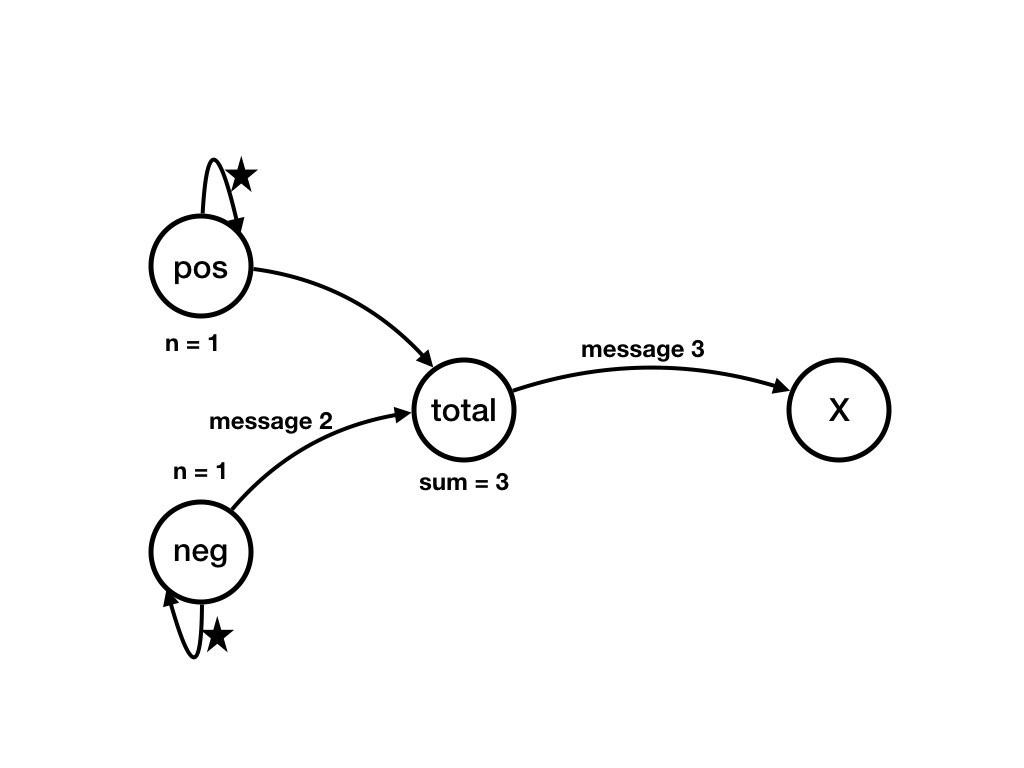
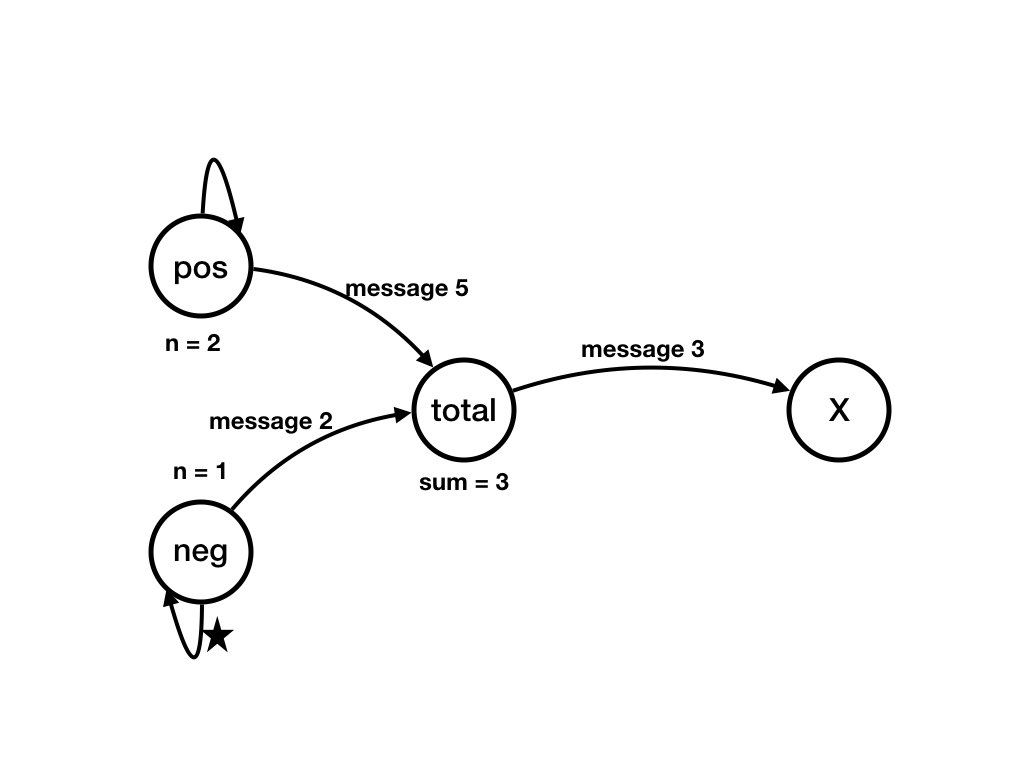
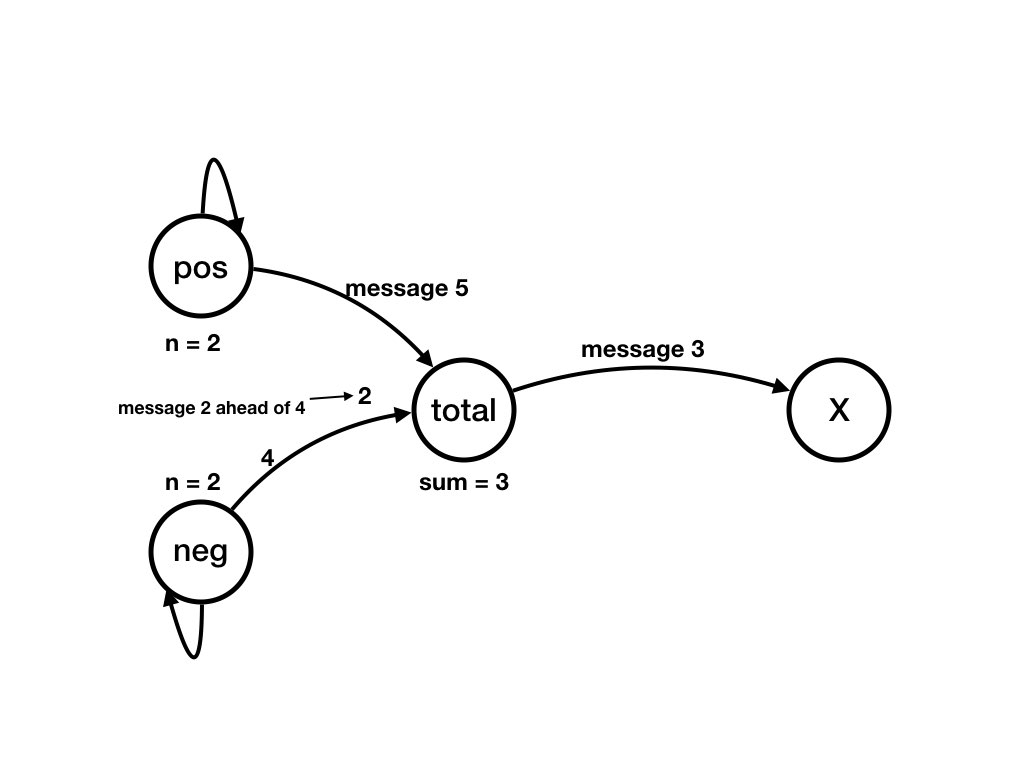
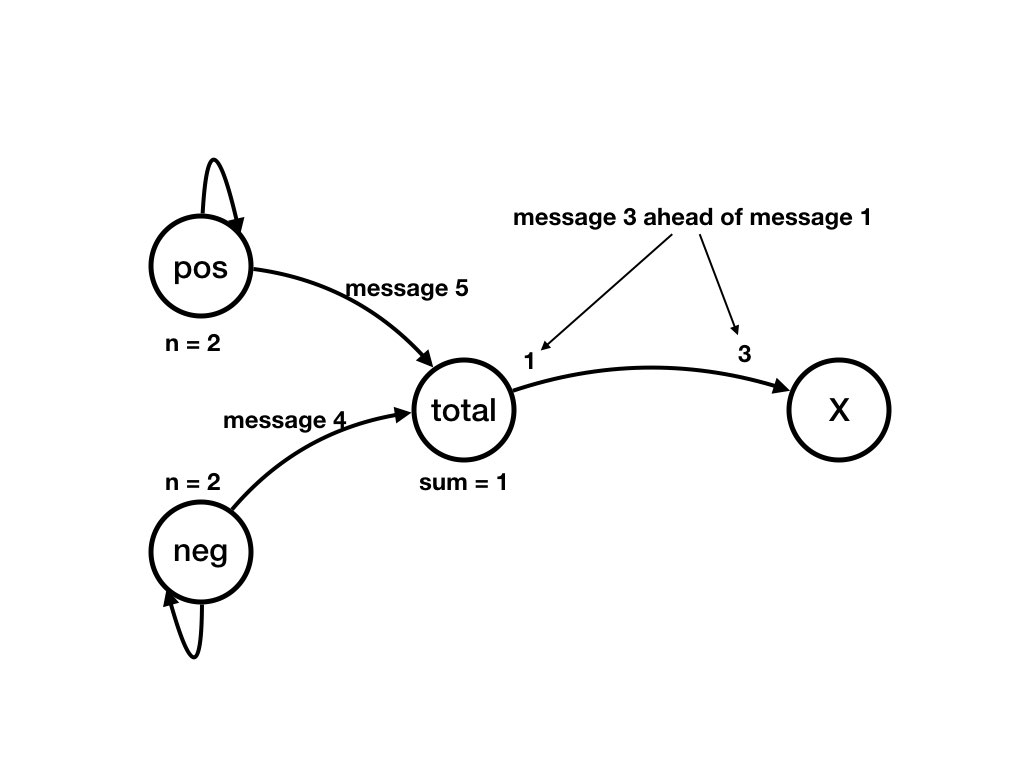
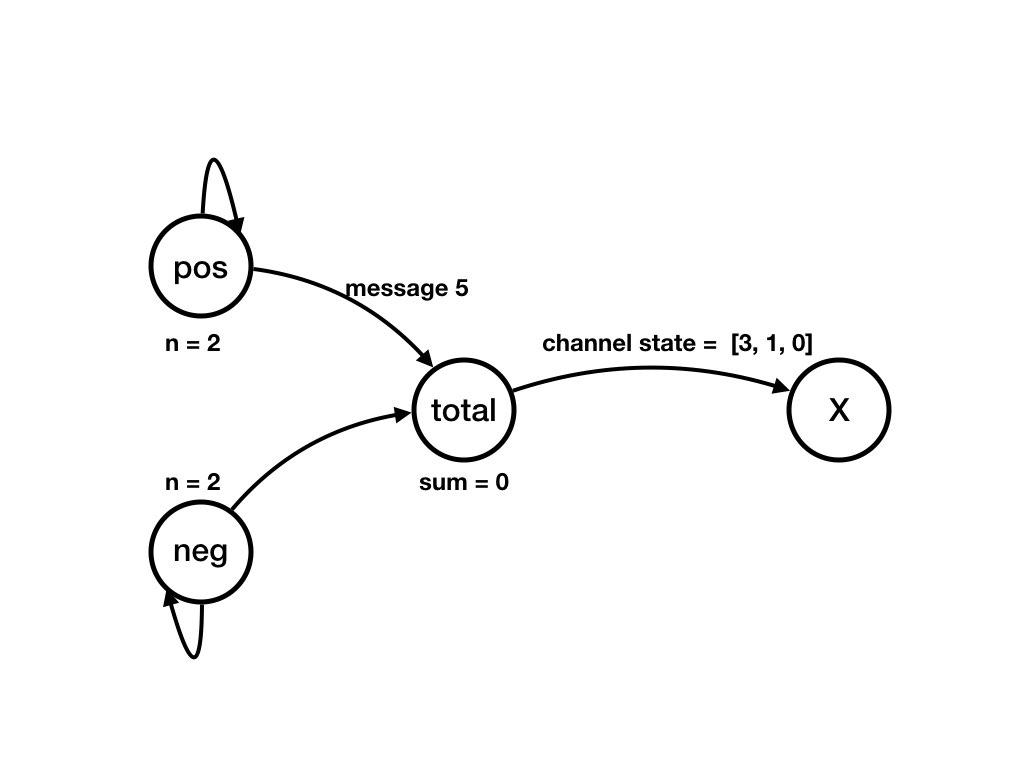
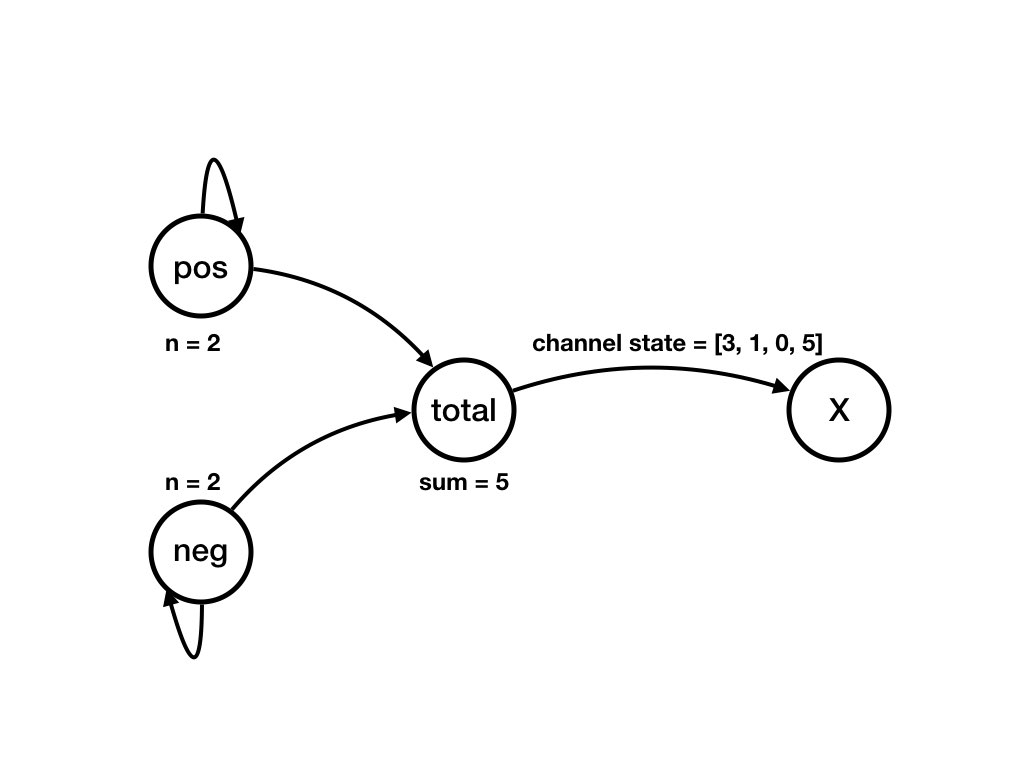
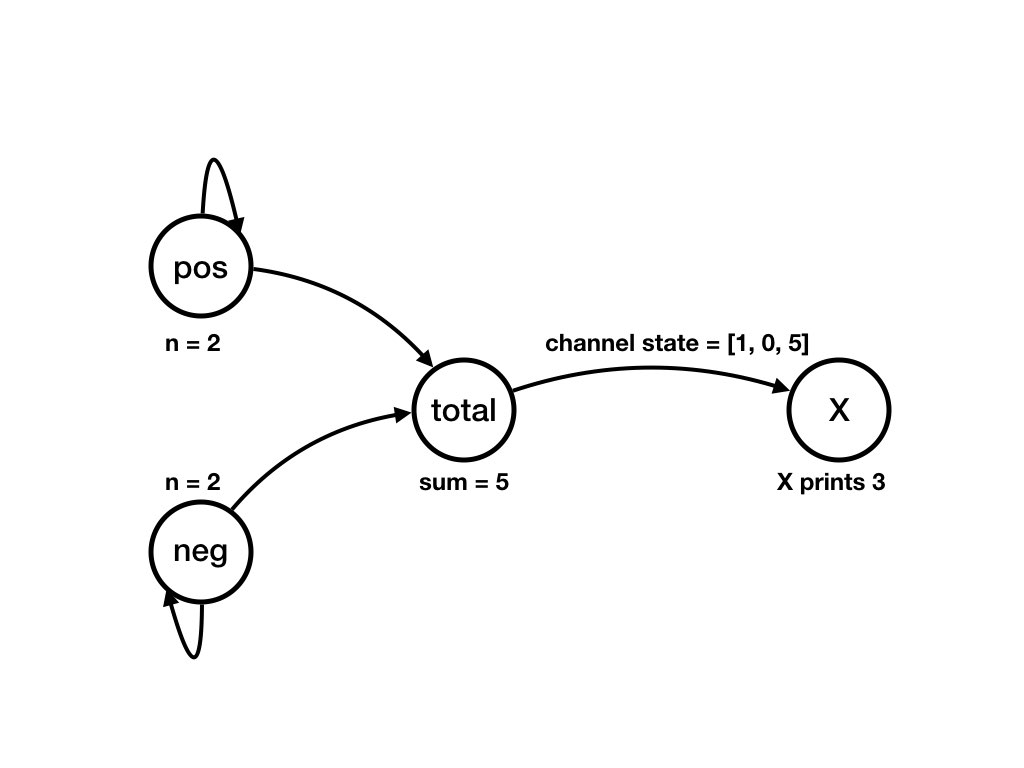
Invariants, Loop Variants and Termination in the Simple Balloon Example

Question

Give an example of an invariant for the balloon example.

Answer

An invariant of the system is:

Number of balloons is at most 2

which is equivalent to: (X, Y) + (Y, X) <= 2

(Here we are abusing notation using (X, Y) for a channel and also for the state of the channel.)

Question

How do you prove that this condition is invariant?

Answer

To prove that this predicate (Boolean condition) is an invariant we prove that (1) it holds initially and (2) and for all state transitions, if the invariant holds in the state before the transition then it holds in the state after the transition.

Initially: (X, Y) = 1 and (Y, X) = 1 So, the predicate holds initially.

A state transition in which a balloon is returned does not change the value of (X, Y) + (Y, X).

A state transition in which a balloon is popped decreases (X, Y) + (Y, X).

Therefore if the predicate holds before a state transition then it holds after the transition.

Question

Is the following an invariant of the system?

((X, Y) + (Y, X) = 2) or (nX = 0) or (nY = 0)

Answer

Yes, this predicate is an invariant.

To prove that this predicate is an invariant we prove that (1) it holds initially and (2) and for all state transitions, if the invariant holds in the state before the transition then it holds in the state after the transition.

Initially, (X, Y) = 1 and (Y, X) = 1. Therefore the predicate holds initially.

Let S be the state before a transition to a state S'. We will prove that if the predicate holds in S then the predicate holds in S'.

Consider two cases:

1. nX = 0 or nY = 0 in S.

   Because nX and nY do not increase, and nX and nY do not become negative, in the execution of an event, it follows that nX = 0 or nY = 0 in S'. Therefore the predicate holds in S'.

2. nX > 0 and nY > 0 in S.

   Because the invariant holds in S it follows that (X, Y) + (Y, X) = 2 in S.

   Because nY > 0 the execution of an event in which Y receives a balloon leaves (X, Y) + (Y, X) unchanged.

   Because nX > 0 the execution of an event in which X receives a balloon leaves (X, Y) + (Y, X) unchanged.

   Therefore (X, Y) + (Y, X) = 2 in S'. So, the predicate holds in S'.

Example of a Loop Variant

Question

How do you prove that the algorithm terminates?

Answer

To prove that the algorithm terminates we use the loop variant: nX + nY + (X, Y) + (Y, X)

The loop variant is a function of the state (i.e. variables) of the system. In this example, the loop variant maps states of the program to integers.

We must show that (1) the loop variant is bounded below and we can carry out induction on the values of the loop variant, i.e., it can decrease only a finite number of times before it reaches a lower bound, and (2) the executions of all steps in all computations that start at initial states reduce the value of the loop variant. The specific lower bound is irrelevant for the proof of termination.

In this example, 0 is (obviously) a lower bound. Next we show that the execution of any event in any state reduces the value of the loop variant.

When Y receives a balloon if nY is positive then nY decreases which the loop variant, and if nY is 0 then (X, Y) which decreases the loop variant.

Similarly every event in which X receives a balloon also reduces the loop variant. Thus the executions of all events reduce the loop variant.

Therefore the algorithm terminates execution.

Question

What can you prove about the state of the system when the computation terminates? We have shown that computations terminate and we given examples of invariants.

Answer

At termination all channels are empty. Let's prove that nX or nY is 0 at termination.

From the invariants if:
(X, Y) + (Y, X) \(\neq\) 2 then nX or nY is 0.

At termination, (X, Y) + (Y, X) \(=\) 0, and the result follows.

More Examples of Invariants and Loop Variants

We reason about the correctness of many distributed algorithms in in the same way that we reason about sequential while loops, by using invariants and loop variants.

Example: GCD using a While Loop

A loop invariant is an assertion about the state of the program that holds before and after each iteration of the loop. You can look up many examples of loop invariants on the web.

Example: Invariant

A loop invariant in the following greatest common divisor (gcd) program is shown in the body of the loop as the assertion gcd(x, y) = gcd(X, Y).

x, y = X, Y
while x != y:
  # assertion: gcd(x, y) = gcd(X, Y)
  if x > y: x = x - y
  else: y = y - x
  

Invariant of a Distributed System for GCD

An invariant of a distributed system is a predicates that holds in all states reachable from initial states. An invariant of a distributed system is the loop invariant of the following while loop. An invariant Inv is shown as an assertion in the body of the loop.

while there exists a nonempty input channel in the system:
   # assertion: Inv
   select a nonempty channel (u, v) in the system
   let the head of channel (u, v) be msg
   v executes receive(msg, u)
  

Example of a Distributed GCD

We are given a strongly connected network of agents -- i.e., there is a path from each agent to every other agent. Each agent has a local variable n, which is initialized as a positive integer. Let GCD be the gcd (greatest commond divisor) of the initial values of X.n of all agents X.n. The following distributed algorithm terminates and at termination X.n = GCD for all agents X.n. In the code, successors is the list of successor agents in a network of agents, and the agent only sends messages to its successors.

def receive(message, sender):
   if n != message:
      n = gcd(n, message)
      for successor in successors:
         send(n, successor)

An invariant of the distributed algorithm is as follows. The gcd of:
all messages in channels and X.n for all agents X
is GCD.

Proof

The proof that the assertion holds initially is trivial. Prove that if the assertion holds before any event then it continues to hold after the event.

Let the event be agent A receiving a message m. After the event, m is no longer in the channel; n = gcd(n, m); and messages with the new value of n are in the output channels from A. The proof that the assertion continues to hold in the post-event state is straightforward.

Example of an Invariant

Another invariant for the gcd example, given earlier, is as follows. For all channels (X, Y) in the network:

1. Channel (X, Y) is empty and X.n is a multiple of Y.n, or
2. The last message in channel (X, Y) is m where m = X.n.

Proof

The assertion holds initially because the second condition holds. Prove that if the assertion holds before any event then it continues to hold after the event.

When agent X executes a receive that changes X.n the agent sends a message m to Y where m = X.n, and so the second condition holds.

When agent Y receives m the agent sets Y.n = gcd(Y.n, m), and so m is a multiple of the new value of Y.n. If channel (X, Y) remains nonempty then the second condition holds. If (X, Y) becomes empty then the first condition holds because m = X.n and m is a multiple of Y.n.

Loop Variant

Question about Loop Variant in the Sequential GCD

What is an example of a loop variant for the following loop?

x, y = X, Y
while x != y:
  # assertion: gcd(x, y) = gcd(X, Y)
  if x > y: x = x - y
  else: y = y - x
  

Answer

f(x, y) = x + y is an example of a loop variant for the following reasons.

1. f is a function of the state of the program.
2. f has integer values.
3. f is bounded below. The bound is 2 because x and y are bounded below because of the invariants x \(\geq\) 1, and y \(\geq\) 1. The precise bounds don't matter.
4. Each execution of the loop decreases f.

We can carry out an induction on f because f has integer values and is bounded below.

Question about Loop Variants in Distributed Algorithms

Let's look at the example of the distributed algorithm given earlier? The example is repeated below.

We are given a strongly connected network of agents -- i.e., there is a path from each agent to every other agent. Each agent has a local variable n, which is initialized as a positive integer. Let GCD be the gcd (greatest commond divisor) of the initial values of X.n of all agents X.n. In the code, successors is the list of successor agents in a network of agents, and the agent only sends messages to its successors.

def receive(message, sender):
   if n != message):
      n = gcd(n, message)
      for successor in successors:
         send(n, successor)

Question

What is an example of a loop variant for the distributed algorithm?

Answer

Let f be the tuple (N, M) where N is the sum of X.n for all agents X, and M is the total number of messages in channels.

Comparisons of tuples are made lexicographically. For example (2, 1) > (1, 10), and (2, 1) < (2, 2).

f is bounded below by (0, 0).

An induction can be carried out on a tuple of integers. Next we show that the execution of each event reduces f.

When an agent X receives a message m,

1. if X.n \(\neq\) m then X.n becomes gcd(X.n, m), and so the new value of X.n is less than its previous value, and so execution of the event decreases N which decreases f.
2. if X.n \(=\) m then the event removes message m from a channel and does not add messages to channels. So the event decreases M which decreases f.

Termination Condition of a While Loop

What can we say about the state at termination of the while loop in the gcd example:

x, y = X, Y
while x != y:
  # assertion: gcd(x, y) = gcd(X, Y)
  if x > y: x = x - y
  else: y = y - x
  

The while loop terminates when x = y. From the invariant, at termination:

gcd(x, y) = gcd(x, x) = x = gcd(X, Y)

Therefore x and y are gcd(X, Y) at termination of the while loop.

Termination Condition of a Distributed Algorithm

What is the termination condition of the distributed gcd algorithm in which the receive of each agent is as follows?

def receive(message, sender):
   if n != message:
      n = gcd(n, message)
      for successor in successors:
         send(n, successor)

At termination all channels are empty. From the invariant, if channel (X, Y) is empty then X.n is a multiple of Y.n.

Therefore when all channels are empty, for every channel (X, Y) in the system X.n is a multiple of Y.n. Because the directed graph of agents and edges specified as successors of agents is strongly connected:

for all agents X, Y in the system: X.n is a multiple of Y.n

Therefore X.n = Y.n for all agents X, Y. From the invariant, X.n is GCD.

Next

The next webpage discusses data flow in computations.

Frequenty Asked Questions

---

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology