A Model of Distributed Systems
This page describes a simple model and notation for distributed algorithms. Other models are introduced later.
Introduction
Distributed systems are complex. Banking systems support tens of thousands of ATM machines, have thousands of branches offices, and serve millions of customers. An earthquake monitoring system has thousands of sensors and agents carrying out complex calculations. Distributed systems provide many services continuously at multiple locations. This course describes algorithms that help in building robust and efficient distributed systems.
Models
A model of a system is an abstraction of the system. A model ignores some features of the system and retains features that are necessary to solve the problem at hand. The choice of a model is an engineering decision: We choose a model that is adequate to solve our problem. Different models are used to design algorithms in different settings; for example, a model of a system in which messages may be corrupted is different from one in which messages are incorruptible.
Notation
The model and its mathematical properties are critical for describing and proving the correctness of algorithms; a programming notation is not important. We need a notation, however, to provide examples. Examples of some algorithms are given in Python using a simulator of distributed systems and also by using software libraries such as a Python implementation of the Advanced Message Queuing Protocol (AMQP). Algorithms are described in plain text or pseudo code in a manner that allows for straightforward implementations using message queuing libraries.
A Simple Model: A Network of Agents and Channels
We begin with a description of a simple actor model and notation. More powerful models are introduced later.
In the simple model, a distributed system consists of a set of agents and a set of channels. A channel is directed from exactly one agent to exactly one agent. The network of agents and channels that constitute a distributed system can be represented by a directed graph in which the vertices represent agents and the directed edges represent channels.
A distributed system is initiated with sets of agents and channels that remain unchanged. Agents and channels are not created or deleted.
Message Communication: Channels
In the simple model, a channel is directed from exactly one agent
to exactly one agent.
A channel from an agent P to an agent Q
is represented by the ordered pair (P, Q).
In the simple model, there exists at most one channel from an
agent P to an agent Q.
There are models that allow more than one channel from one agent
to another; however, for the time being we restrict ourselves to
the simple model.
A channel (P, Q) is called an output of agent
P and an input of agent Q.
The sender and receiver of a channel (P,
Q) are P and Q, respectively.
An agent can send messages only on its output channels and receive
messages only on its input channels.
The state of a channel is a queue of messages -- these are the messages that have been sent on the channel and that have not been received.
An agent sends a message on a channel by appending the message to the tail of the queue of messages in transit along the channel. A message from a nonempty channel is delivered to an agent by removing the message from the head of the queue of messages in the channel, and passing the message to the agent.
In the simple model, channels have unlimited capacity. The queue that represents the state of a channel has unbounded size. A sender is never blocked from sending messages on a channel.
Messages sent on the same channel are delivered in the order sent.
If an agent P sends a message M1 on a
channel (P, Q), and later sends a message M2
on the same channel, then agent Q receives
M1 on channel (P, Q) before Q
receives M2 on the channel.
Messages Sent on Different Channels may be Delivered out of Order
Messages sent on different channels may not be delivered in the order sent. The following scenario (see figure) is possible with different agents \(A, B, C\).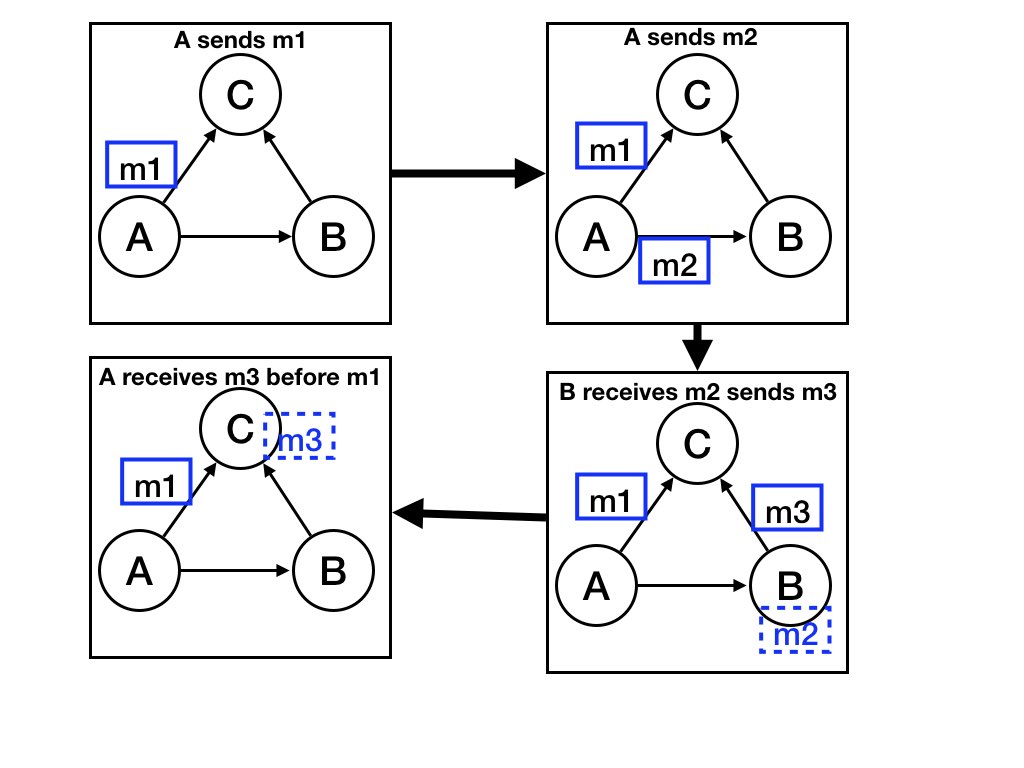
- \(A\) sends message \(m_{1}\) to \(C\).
- Then \(A\) sends message \(m_{2}\) to \(B\).
- When \(B\) receives \(m_{2}\), \(B\) sends a message \(m_{3}\) to \(C\).
- \(C\) receives \(m_{3}\) before \(C\) receives \(m_{1}\).
Agents
An agent is an object that can send messages to, and receives messages from agents. An agent is either waiting to receive a message or is processing a message that it has received. An agent that is waiting starts processing a message when the agent receives a message. When an agent finishes processing a message the agent waits for the next message to be delivered to it.
Each agent has a set of variables. An agent's variables are local to the agent -- they cannot be accessed by other agents. A message sent by an agent cannot be a pointer into the agent's memory.
An agent is specified by (1) statements that initialize the agent's variables and (2) a function
receive(message, sender)called a callback function in message queuing libraries.
If the system has a waiting agent u with a nonempty
input channel (v, u) then the system may
remove the message m at the head of
(v, u), and call
the receive(message, sender) function of u
where message is m and sender
is v.
In the simple model, an agent does not choose the channel from which the agent receives its next message. The system chooses any nonempty channel from which it delivers a message to the receiver of that channel. A waiting agent cannot refuse to accept a message.
A receive function must not be recursive: an agent cannot
receive a new message while it is processing a message.
Every execution of receive must terminate.
An agent is not interrupted while it is executing a
receive.
An agent may have many nonempty input channels but the agent processes
only one message at a time. Messages that arrive while an
agent is executing a receive remain in channels.
After an agent completes execution of a receive the agent
returns to waiting state.
An agent may send messages in its receive function.
An agent sends a message by executing
send(message, receiver)The first parameter of
send is the message that is sent,
and the second paramenter is the agent to which the message is sent.
Execution of this statement places the message in the output channel
directed from the sender to the receiver.
Agents implemented in most programming
languages are deterministic.
The statements that initialize an agent are deterministic
and so an agent has a single initial state.
Multiple executions of a receive function with the same
input produce the same output.
The theory of distributed systems does not require agents to be
deterministic.
For the time being we consider only deterministic agents.
See examples and
code
We discuss nondeterministic agents later.
Examples
Example of a System
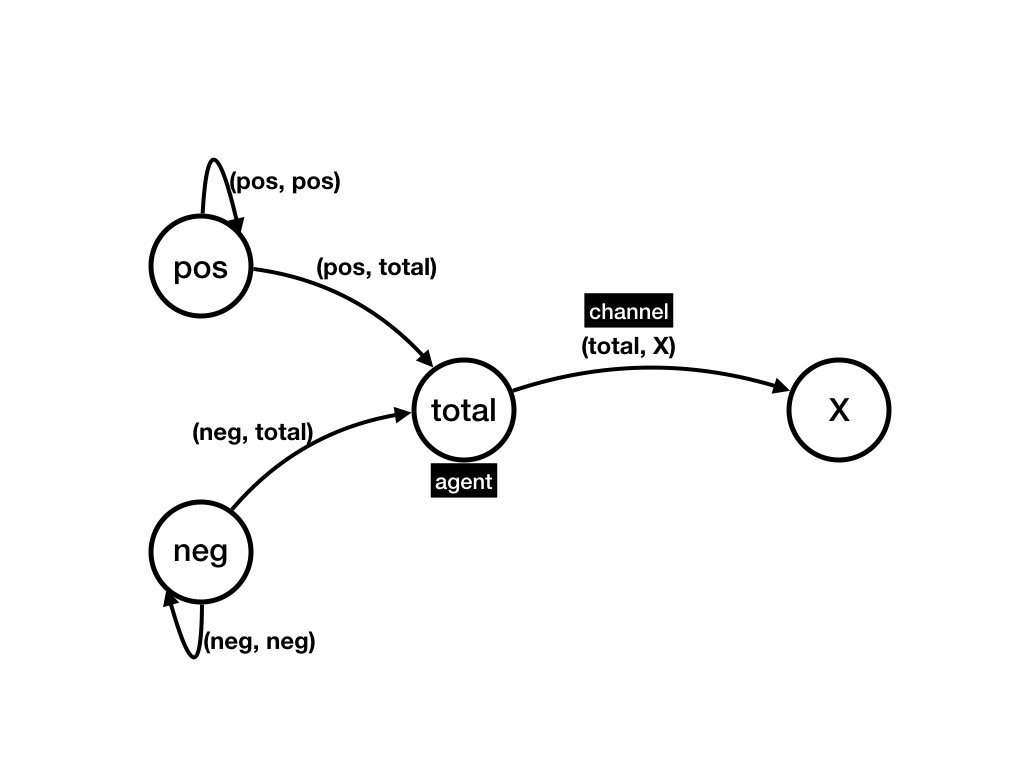
A system has 4 agents,pos, neg,
total, and X.
The channels in the system are
(pos, pos),
(neg, neg),
(pos, total),
(neg, total), and
(total, X).
See "Figure Agents and Channels" which shows the network of
agents and channels represented as a directed graph.
Examples of Agents
This is an example of an agent,total,
that receives messages from agents
pos and neg,
and sends messages to agent X.
See an example
of an implementation in Python using an Agent class.
The example below does not use classes so that the algorithm is easier
to understand by readers who are not familiar with Python.
An agent is specified by a block of statements that initialize the
variables of the agent and the initial messages (if any) in
the agent's output channels, and the receive function.
The block of statements before the receive function
initialize the agent.
In this example, the agent total has a single
variable sum which has value 0 initially.
Initially, the output channel of total is empty
# Algorithm for total
# ------- Initialization --------------
sum = 0
# ------- receive function ----------
def receive(message, sender):
if sender == pos:
sum = sum + message
else:
sum = sum - message
if sum < 0: sum = 0
send(sum, X)
If total receives a message from pos then
total
increments sum by the contents of the message.
If total receives a message from an agent other than
pos then total decrements sum by the
contents of the message, and if the resulting value of
sum is negative then sum is set to 0.
total sends the
resulting value of sum to agent X.
Example of pos
This is an example of agent pos.
# Algorithm for pos
# -------- Initialization --------------
my_data = [3, 5]
n = 0
send(message="wakeup", receiver=pos)
# ------- receive function ----------
def receive(message, sender):
send(message=my_data[n], receiver=total)
n = n + 1
if n < len(my_data):
send(message="wakeup", receiver=pos)
pos has variables my_data and n
which are initially [3, 5] and 0,
respectively.
Initially there is a message "wakeup" in the channel from
pos to itself.
When pos receives a message it sends
my_data[n] to agent total and then
increments n.
If n is less than the number of elements in
my_data then pos sends itself a "wakeup" message.
The system is initialized with a "wakeup" message in the channel from
pos to itself.
When pos receives the first message it sends
my_data[0] to agent total,
increments n to 1
and pos sends another "wakeup" message to itself.
When pos receives the next message it sends
my_data[1] to agent total, and
increments n to 2, and does not send itself a message.
So, in this example, pos waits forever after this point
because it receives no further messages.
In this example, agent neg is identical to
pos except that it
may have different values of my_data,
Agent X has no variables. It merely prints
messages that it receives.
Next
The next page defines states, state transitions, timelines and dataflow in distributed systems.K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology