Basics: Examples

Please look at the Python examples that use the Agent class in addition to the examples below.

Basics: Examples Movies

10-second MP4 movie: Messages sent in different channels may be delivered out of order.

Question

A system has agents \(A\), \(B\), and \(C\). Initially the channel from \(A\) to \(A\) contains a "wakeup" message. All other channels are empty.

Ignore the states of agents for the purposes of this question. Is the following scenario possible?

1. Agent \(A\) receives a wakeup message and sends a message \(m_{1}\) to \(C\) and a wakeup to itself.
2. Agent \(A\) receives a wakeup message and sends a message \(m_{2}\) to \(B\).
3. Agent \(B\) receives \(m_{1}\) from \(A\) and sends a message \(m_{3}\) to \(C\).
4. Agent \(C\) receives \(m_{3}\) from \(B\).
5. Agent \(C\) receives \(m_{2}\) from \(A\).

Answer

Yes, the scenario is possible. Messages sent on a channel are delivered in the order sent on that channel. Messages sent on different channels may not be received in the order sent on those channels.

Question

A system has agents \(A\) and \(B\). Initially the channel from \(A\) to \(A\) contains a "wakeup" message. All other channels are empty.

Ignore the states of agents for the purposes of this question. Is the following scenario possible?

1. Agent \(A\) receives a wakeup message and sends a message \(m_{1}\) to \(B\) and a wakeup to itself.
2. Agent \(A\) receives a wakeup message and sends a message \(m_{2}\) to \(B\) and a wakeup to itself.
3. Agent \(B\) receives \(m_{2}\) from \(A\)
4. Agent \(B\) receives \(m_{1}\) from \(A\)

Answer

No, the scenario is not possible. Messages sent on a channel are delivered in the order sent on that channel. So \(A\) receives \(m_{1}\) from \(B\) before it receives \(m_{2}\) from \(B\).

Example of a System

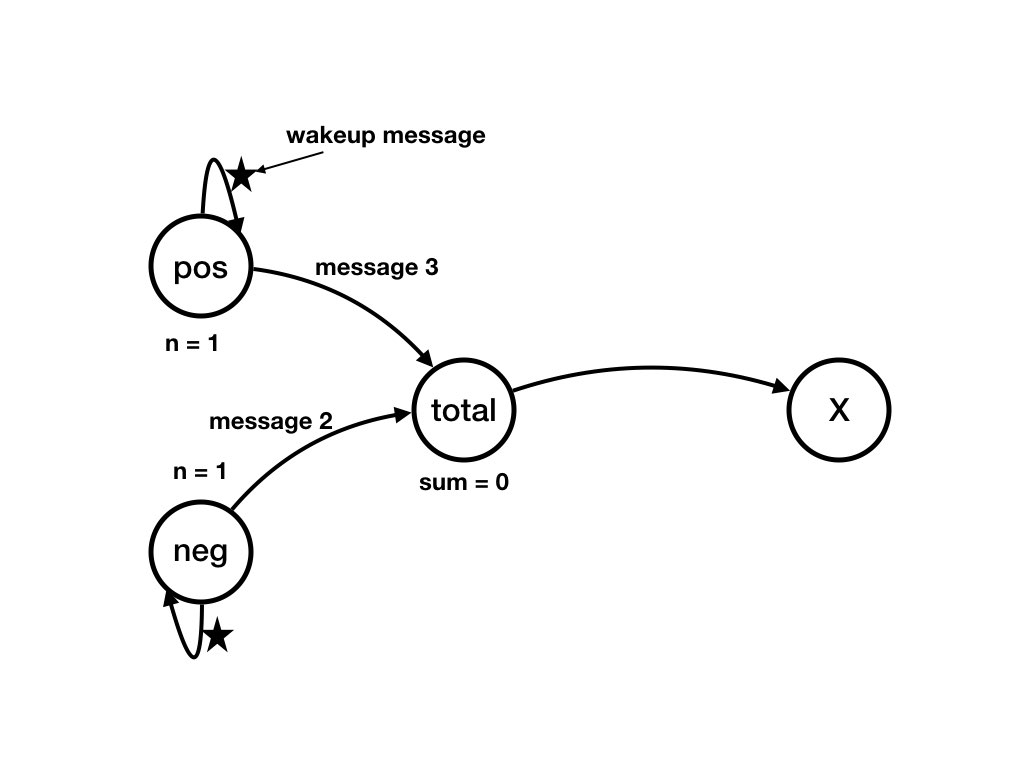
Consider the example given in the previous page. Assume that agent neg is the same as agent pos except that neg.my_data = [2, 4] At some point message 3 is in channel (pos, total) and message 2 is in channel (neg, total), and these are the only messages in these channels. There is a wakeup message in channel (pos, pos) and in channel (neg, neg).

See Figure Agents and Channels Example 1.1

Question

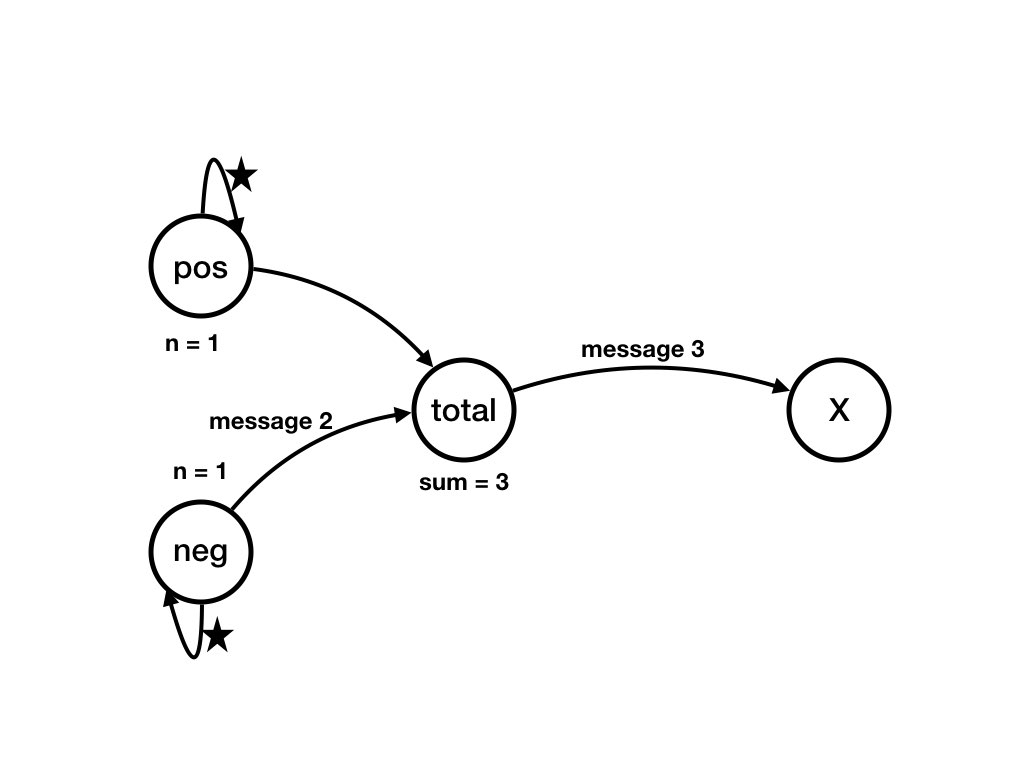
What changes occur if agent total receives the message from pos and this is the first message that total receives?

Answer

The message 3 on channel (pos, total) is removed from the channel. Agent total's variable sum becomes 3 and channel (total, X) contains message 3.

See Figure Agents and Channels Example 1.2

Question

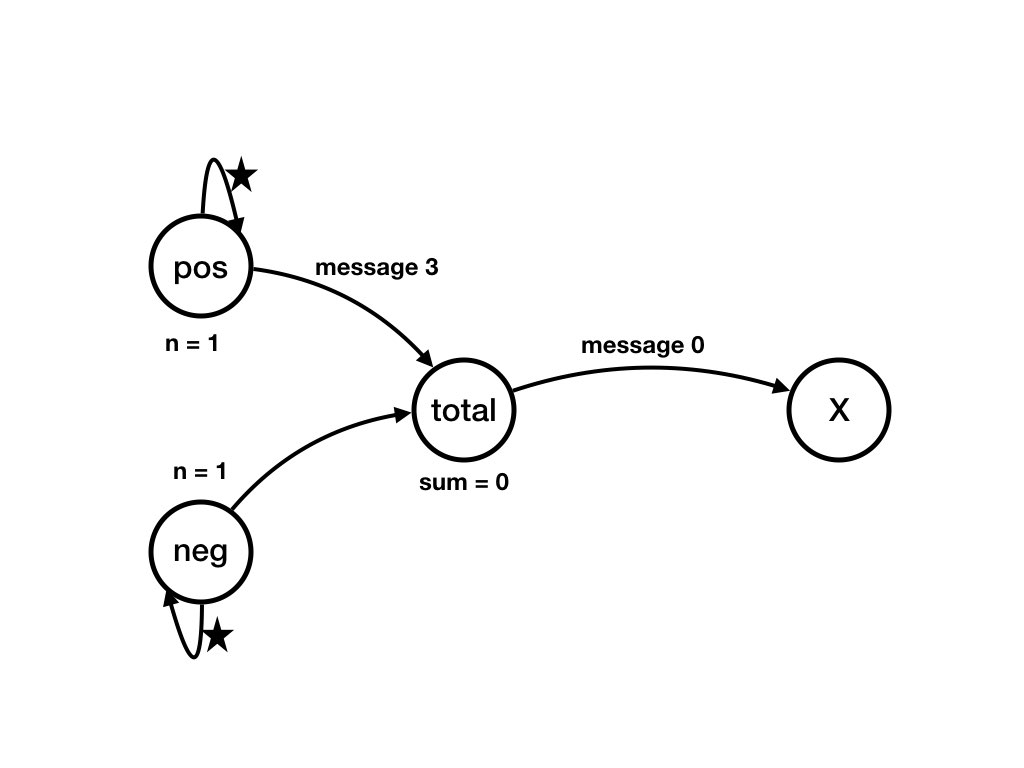
Same initial state as in the previous question. What changes occur if agent total receives the message from neg and this is the first message that total receives?

Answer

The message 2 on channel (neg, total) is removed from the channel. Agent total's variable sum becomes 0 and channel (total, X) contains message 0.

See Figure Agents and Channels Example 1.3

Question

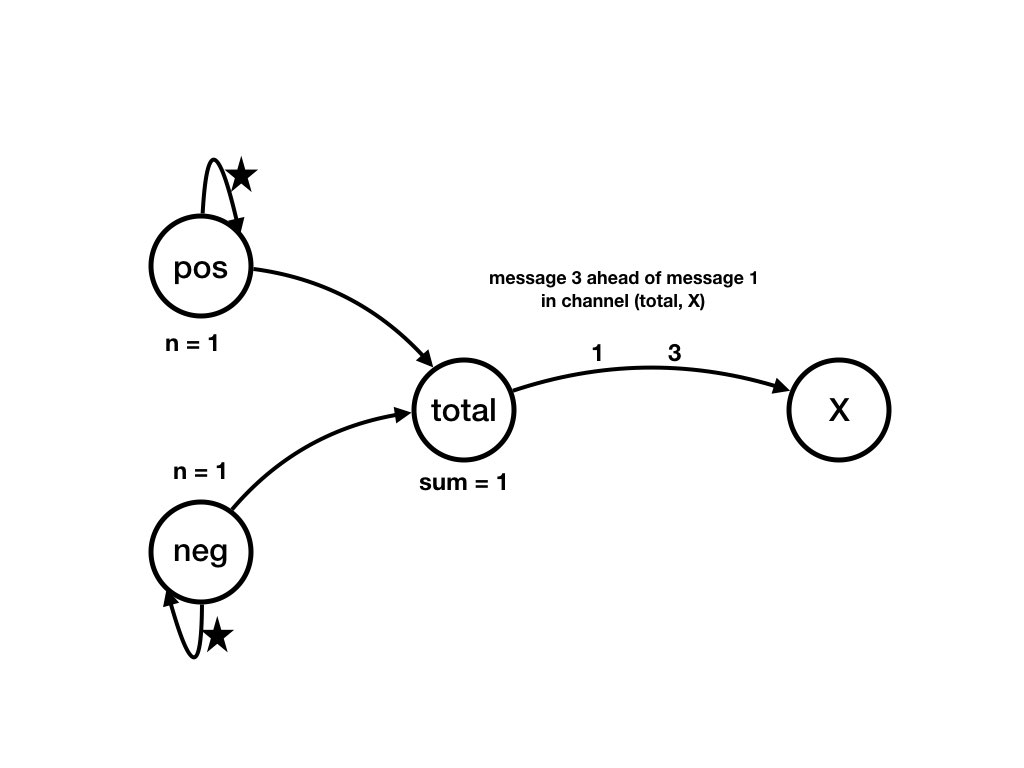
Same starting state as in the previous two questions. What changes occur if agent total receives the message from pos and then from neg?

Answer

After agent total receives the message from pos and then from neg the channels from pos and neg to total are empty, and the channel from total to X contains message 3 followed by message 1, and agent total's variable sum is 1.

See Figure Agents and Channels Example 1.4

Question

What changes occur if agent total receives its first message from neg and its second from pos?

Answer

After agent total receives the message from neg and then from pos the channels from pos and neg to total are empty, and the channel from total to X contains message 0 followed by message 3, and agent total's variable, sum, is 3.

See Figure Agents and Channels Example 1.5

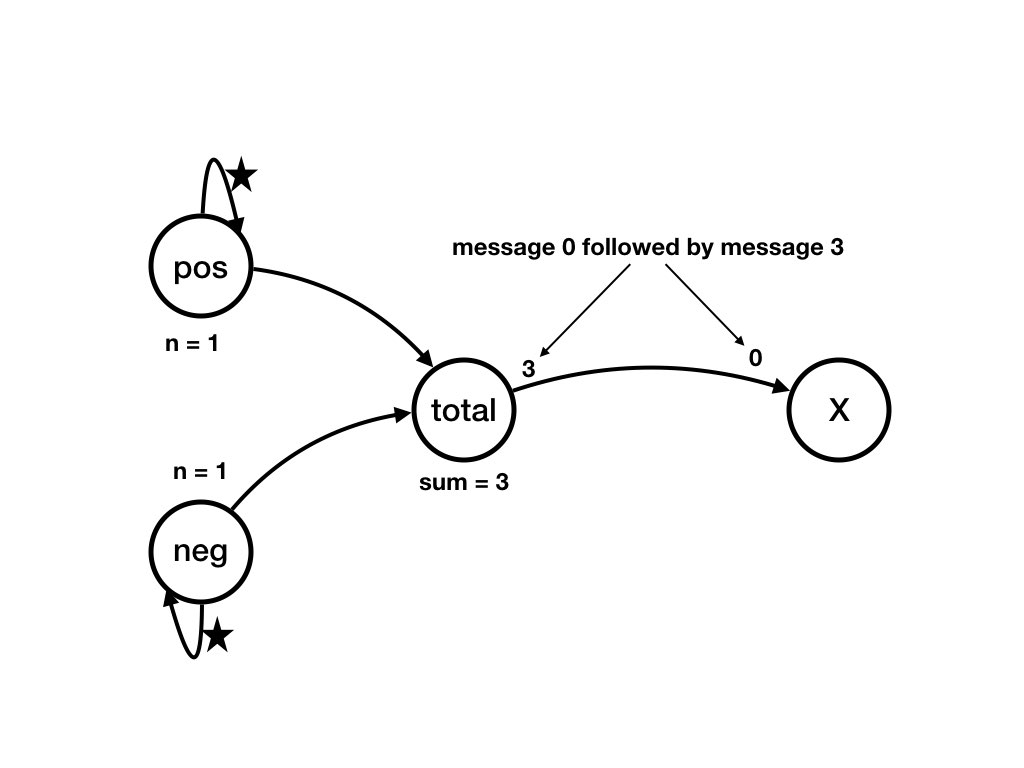
Question

Consider a sequence of state changes that ends in a state in which all agents are waiting and all channels are empty. Agent X prints the messages that it receives. What does X print during this sequence of state changes?

Answer

X may print any of the following:

1. 3, 8, 6, 2.

   If total receives 3, 5 from pos and then receives 2, 4 from neg.

2. 3, 1, 6, 2.

   If total receives 3 from pos, then 2 from neg, then 5 from pos, then 4 from neg

3. 3, 1, 0, 5.

   If total receives 3 from pos, then 2 from neg, then 4 from neg, then 5 from pos.

4. 0, 3, 8, 4.

   If total receives 2 from neg, then 3 from pos, then 5 from pos, then 4 from neg.

5. 0, 3, 0, 5.

   If total receives 2 from neg, then 3 from pos, then 4 from neg, then 5 from pos.

6. 0, 0, 3, 8.

   If total receives 2 from neg, then 4 from neg, then 3 from pos, then 5 from pos.

Example: Earliest Meeting Time

Central Ideas: Example illustrating model of a distributed system defined by its components (agents, channels), states, state transitions, and computations.

Agents

Three professors (agents) indexed \(0, 1, 2\) want to find the earliest time that all of them are free so that they can schedule an exam for a student. Each professor \(j\) has a local variable \(T_{j}\) where professor \(j\) can meet at time \(T_{j}\).

Associated with each professor \(j\) is a function \(f_{j}\) where for any time \(t\), \(f_{j}(t)\) is the earliest time at or after \(t\) that professor \(j\) can meet. All professors can meet at time \(t\) exactly when for all \(t\):

\( f_{j}(t) = t \)

We assume that there exists some time at which all professors can meet. Otherwise, the student would never get to take the exam! Let the earliest meeting time for all professors be \(\tau\).

Channels

There is a channel from each professor to each of the other professors as shown in the diagram. Let \(c_{j,k}\) be the channel from professor \(j\) to professor \(k\).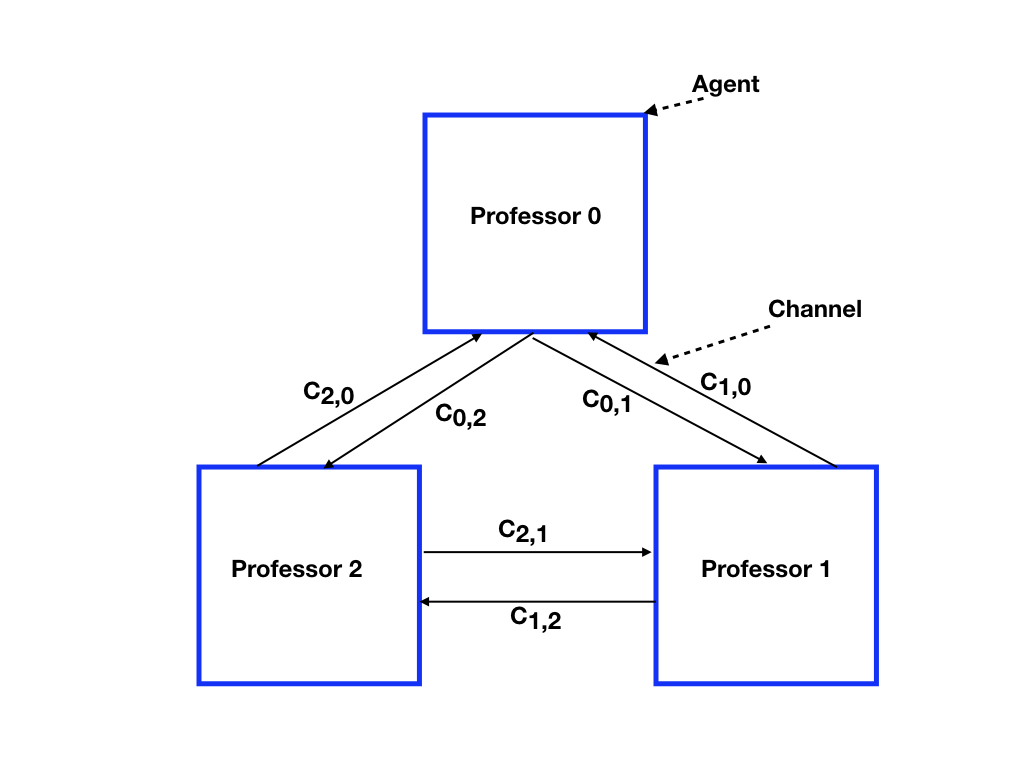

Initial State

Let \(T_{j}^{0}\) be the earliest time that professor \(j\) can meet. Initially \(T_{j} = T_{j}^{0}\) and each of the two channels from professor \(j\) contain a single message \(T_{j}^{0}\).

State Transitions

In this example agents (i.e. professors) have no internal transitions. The only transitions are delivery of messages from channels.

Action on Receiving a Message

Let \(t\) be the message at the head of a channel \(c\) directed towards professor \(T_{j}^{0}\). The program executed when a message t is received is:

upon receiving t:
  if t > T[j]:
     T[j] = f(t)
     send T[j] on all outgoing channels of j
  else:
     pass

The proof that the algorithm terminates with \(T_{j} = \tau\) for all \(j\) is left as an exercise.

A Possible Computation

Assume that professor \(0, 1, 2\) can only meet on days that are postive multiples of 2, 3, and 4, respectively. Then the earliest time that all professors can meet is 12. Let's look at one of may possible system computations.

Initially

Initially the outgoing channels from professors 0, 1, 2 each contain the message \(2, 3, 4\), respectively. Each channel has exactly one message.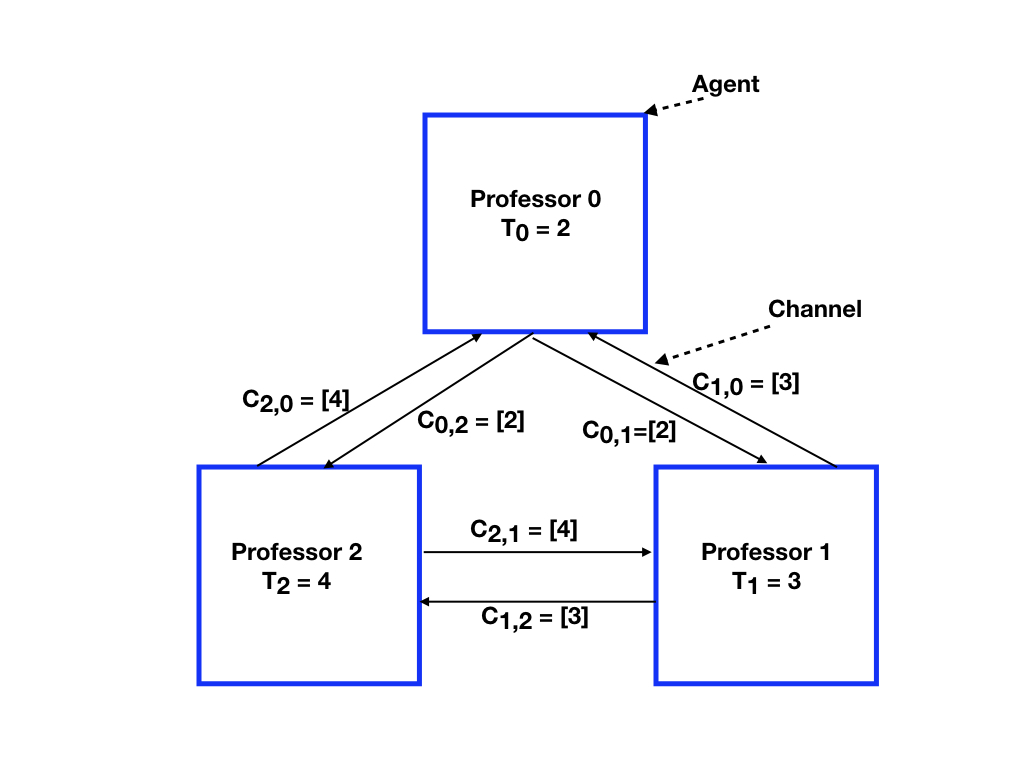

A First Step

Since all the channels are nonempty, the next step can be the delivery of a message from any channel. Assume that message \(4\) in channel \(c_{2, 0}\) is delivered to professor \(0\). The state of professor \(0\) changes because \(T_{0}\) becomes 4, and this professor send message 4 on channel \(c_{0, 2}\), and so the state of this channel becomes the sequence \([2, 4]\) with message \(2\) ahead of message \(4\).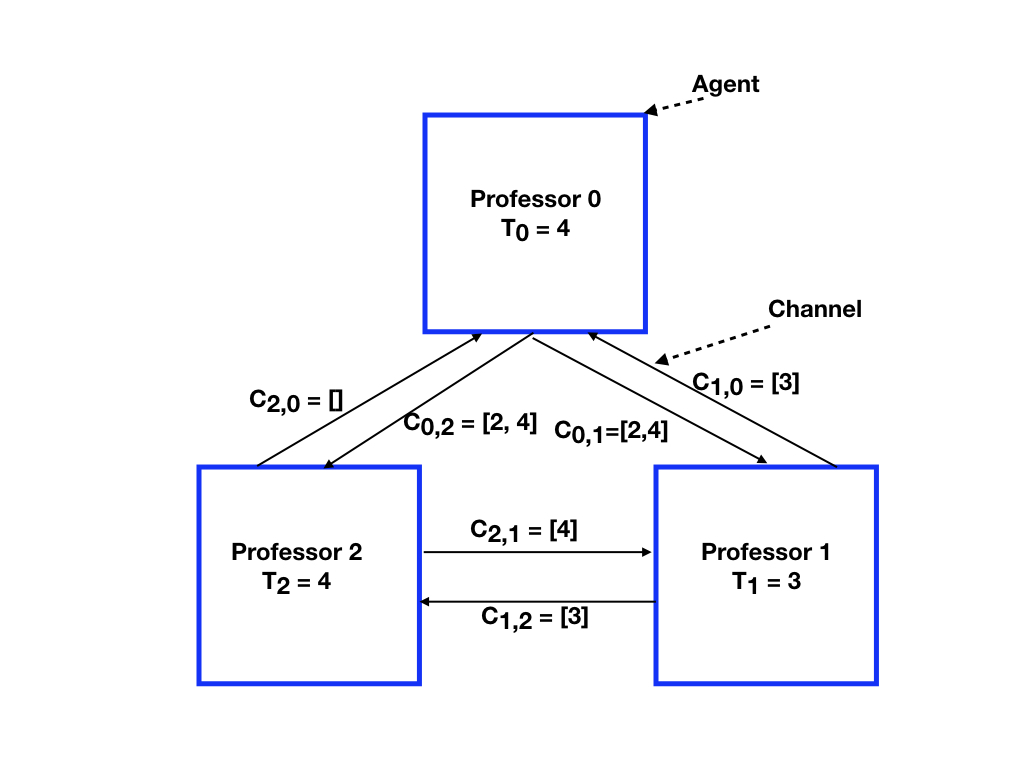

A Second Step

At the end of the first step, channel \(c_{2, 0}\) is false because the channel is empty. Every other channel contains a message. So, the next transition can be the delivery of a message from any channel other than \(c_{2, 0}\). Suppose the next message is delivered from channel \(c_{0, 2}\). This message is 2 because that's the message at the head of the sequence of messages in transit along the channel. Delivery of this message removes the message from the channel, and the execution of this action does not change the state of professor \(2\) because \( (t \leq T[2]) \). The state of channel \(c_{0, 2}\) now consists of a single message \(4\).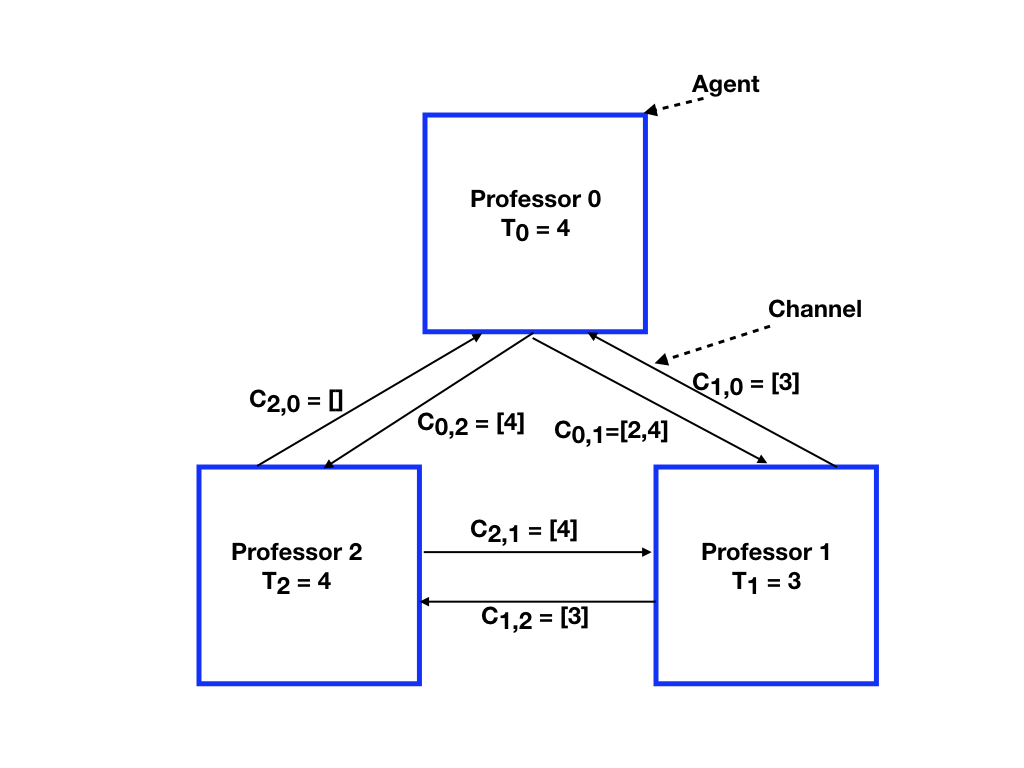

A Third Step

At the end of the second step, all the channels other than \(c_{2, 0}\) are nonempty, and a message can be delivered from any nonempty channel. Suppose the next message delivered is the message \(4\) in channel \(c_{0, 2}\). The delivery of this message does not change the state of professor \(2\), and the action makes channel \(c_{0, 2}\) becomes empty.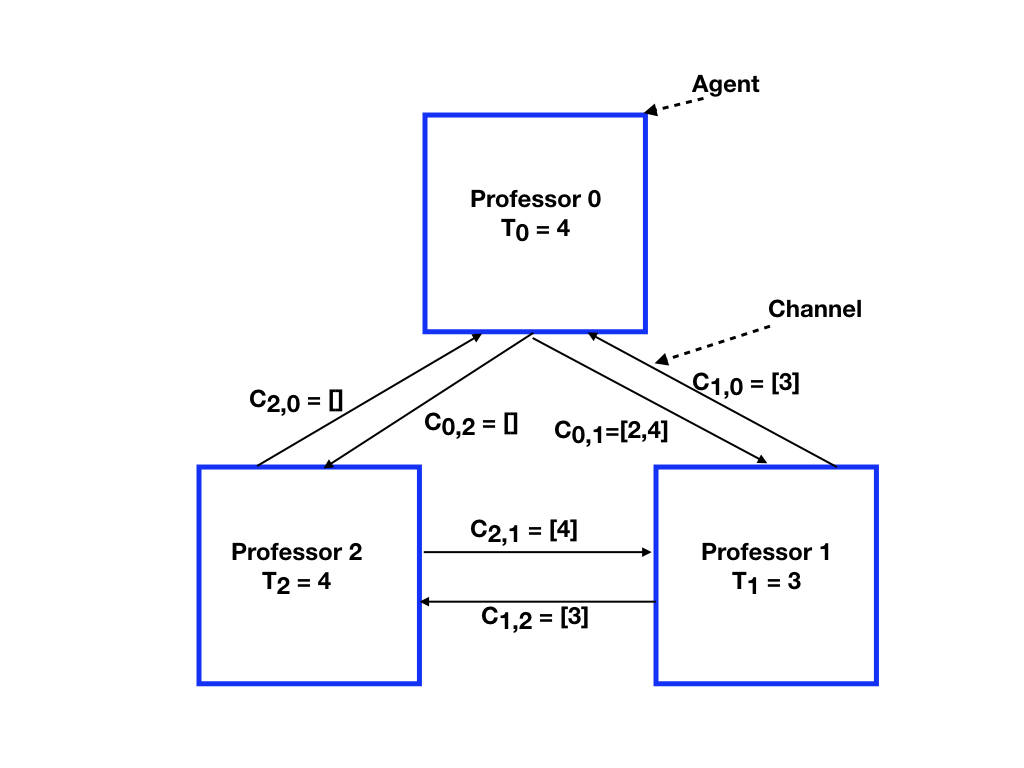

Following Steps

At the end of the third step the only nonempty channels are those to and from professor \(1\). Think about further steps in the computation. The computation proceeds in this manner until all guards evaluate to false, i.e., all channels are empty.

Verify that all computations end in a state in which all channels are empty and \(T_{j} = 12\) for all \(j\).

Self Test

Show that the algorithm is correct for a strongly-connected graph of professors.

Self Test

Each agent \(j\) has a local constant \(T_{j}\) and a local variable \(v_{j}\). Given a strongly-connected agent-channel graph, develop an algorithm that terminates and at termination:

\( v_{j} = \; \textrm{GCD} (\forall k: T_{k}) \) where GCD is the greatest common divisor.

Self Test

Same problem as the previous case except that at termination:

\( v_{j} = \; \textrm{LCM} (\forall k: T_{k}) \) where LCM is the least common multiple.

Self Test

Generalize the results from the self tests to determine a general algorithm which applies to all the previous self tests. The general algorithm has a function \(f_{j}\) that is passed to each agent \(j\).

Optional Implementation

Implement the general algorithm using Python Pika or the Python simulator or any language of your choice.

Next

The next page defines states, state transitions, timelines and dataflow in distributed systems.

---

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology