Logical Clocks and Epochs
A logical clock algorithm assigns a value, called the logical time, to each step in a computation so that every edge in the dataflow graph of the computation is from a vertex with a smaller logical time to a vertex at a higher logical time. So, all sequences of steps in ascending logical time are topological sorts of the dataflow graph, and therefore all sequences of steps in ascending logical time are computations. An epoch is similar to logical time where there exists a computation that is a sequence of steps in ascending epoch. We use epochs in Paxos, a consensus algorithm.
The Problem
We first describe logical time and later describe epochs.Design an algorithm that assigns a value \(t(e)\), called the logical time of \(e\), to each step \(e\) in a computation so that:
The Logical Time Property
For all edges \((e, e')\) of the dataflow graph: \(t(e) < t(e')\).
The standard definition is in terms of causality rather than data flow, but the definitions are equivalent with "step \(e\) causes step \(e'\)" as the same as "there is a path in the dataflow graph from \(e\) to \(e'\)."
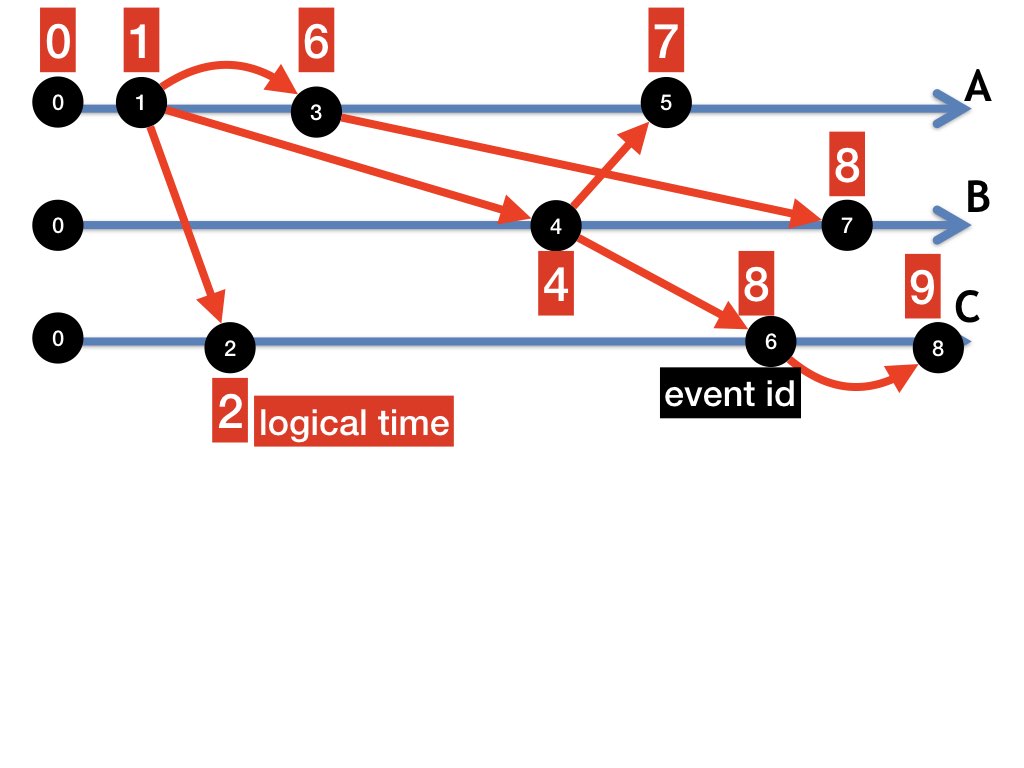
Example: Logical Times of Steps
Figure 1 shows the dataflow graph of a computation with agents \(A, B, C\) and step sequence \([0, 1, 2, \ldots, ]\). The white numbers inside the black vertices are the step ids which show the position of the step in the computation. The red numbers outside the steps are logical times assigned to steps.
Logical times are arbitrary provided every edge is directed from a lower to a higer logical time.
A Logical Clock Algorithm
The following algorithm is suggested by the logical time property.Assigning Logical Times to Steps
For any step \(e\) at any agent \(x\), let \(e'\) be the step immediately preceding \(e\) at \(x\) and let the timestamp of the message received in \(e\) be \(T\).
Set \(t(e)\) to be any value greater than max(t(e'), T).
This rule ensures that (1) later steps at an agent have higher logical times than earlier steps at that agent, and (2) a message is received in a step with a higher logical time than the logical time of the step in which the message is sent.
Theorem
All sequences of steps of a dataflow graph in ascending order of logical time are computations.Proof
For any edge \((e, e')\) in the dataflow graph, \(t(e) < t(e')\). In a sequence of steps ascending in time, \(e\) appears before \(e'\), and so the sequence is a topological sort of the dataflow graph, and therefore the sequence is a computation.
Epochs
Design an algorithm that assigns a value \(t(e)\), called the epoch of \(e\), to each step \(e\) in a computation so that:
The Epoch Property
For all edges \((e, e')\) of the dataflow graph: \(t(e) \leq t(e')\).
The only difference between logical time and epochs is that strict inequality \(t(e) < t(e')\) in logical time has been replaced by non-strict inequality \(t(e) \leq t(e')\) in epochs.
Epochs of steps are arbitrary provided every edge is directed from a step to a step with the same or higher epoch.
Example: Epochs of Steps
Figure 2 shows an assignment of epochs to steps for the dataflow graph that is also shown in figure 1.The dataflow graph is for a computation C = [0, 1, 2, 3, 4, 5, 6, 7, 8] and the sequence of epochs for this computation is [0, 1, 2, 1, 1, 1, 2, 3, 2], which is not in ascending order. An example of a permutation of the given computation, where the permutation is in ascending order, is C' = [0, 1, 3, 4, 5, 2, 6, 8, 7] and the sequence of epochs is [0, 1, 1, 1, 1, 2, 2, 2, 3].
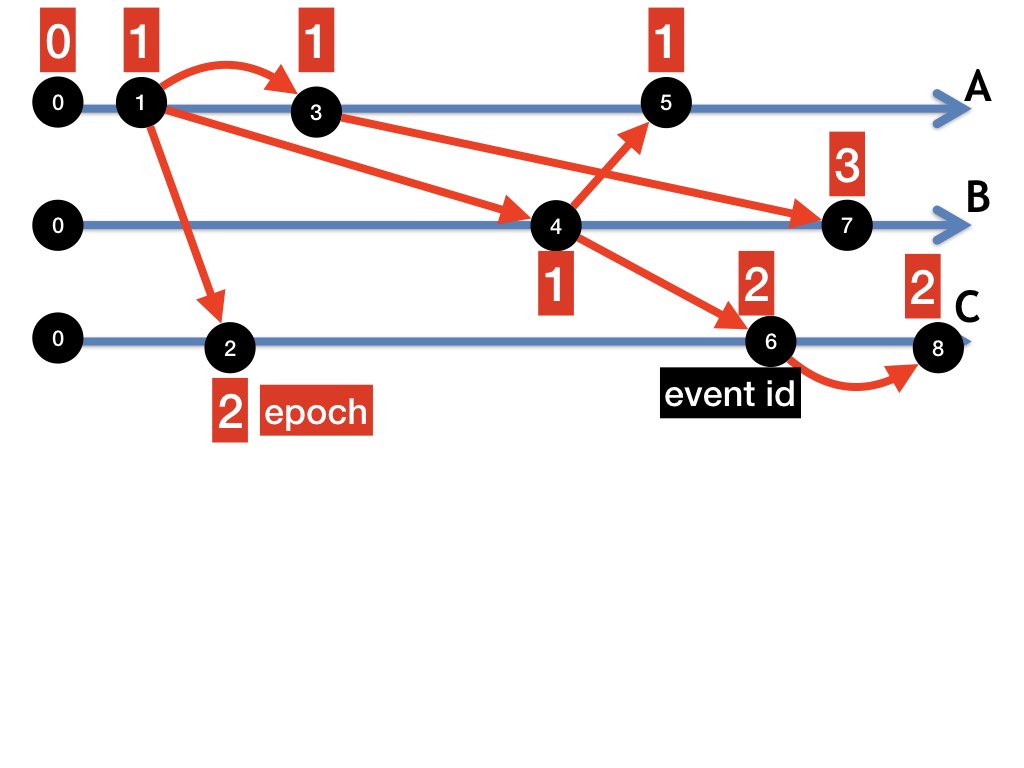
The sequence of steps C' is obtained from C by switching the order of adjacent elements that are not in order. For example, step 2 has a higher epoch than step 3, but step 2 appears before, and adjacent to, step 3 in C. Steps 2 and 3 are independent -- there is no path between them in the dataflow graph -- and so switching them gives a sequence of steps which is a computation. Repeatedly switching the order of adjacent elements that are not in order gives C'.
Observe that for each agent the sequence of steps at the agent is the same in C and C'. For example, the sequence of steps of agent A in both C and C' is [0, 1, 3, 5], and the sequence of steps of agent B in both C and C' is [0, 4, 7].
Rules for Epochs
Epochs are assignments \(t(e)\) to step \(e\) such that for all steps \(e, e'\):
- If \(e\) and \(e'\) occur at the same agent and \(e'\) occurs after \(e\) then \(t(e) \leq t(e')\).
- If \(e\) is a step in which a message is sent and \(e'\) is the step in which that message is received then \(t(e) \leq t(e')\).
Theorem
Let \(C\) be a computation and let \(t(e)\) be the epoch of step \(e\) for each step \(e\) in the computation. There exists a computation \(C'\) where: (1) For each agent \(v\) the sequence of steps at \(v\) is the same in \(C\) and \(C'\), and (2) steps in \(C'\) are in ascending order of epochs.Proof
Let \(G\) be the dataflow graph of \(C\). We will identify a topological sort \(C'\) of \(G\) where \(C'\) satisfies the condition of the theorem. Because all topological sorts of the dataflow graph are computations it follows that \(C'\) is a computation.Let \(C'\) be a permutation of \(C\) where steps in \(C'\) occur in ascending epochs and where steps with the same epoch occur in the same order in \(C\) and \(C'\). Computation \(C'\) can be obtained from \(C\) by repeatedly switching the order of adjacent steps in \(C\) that are not in order.
Let \((e, e')\) be an edge of the dataflow graph of \(C\). Then \(t(e) \leq t(e')\). If \(t(e) < t(e')\) then \(e\) is before \(e'\) in \(C'\) because events in \(C'\) are in ascending epochs. If \(t(e) = t(e')\) then \(e\) is before \(e'\) in \(C\), and therefore \(e\) is before \(e'\) in \(C'\) because the order of steps with the same epoch are identical in \(C\) and \(C'\). So, \(C'\) is a topological sort of \(G\).
Applications of Logical Time and Epochs
Sequences of steps in increasing logical time are computations. Logical times simplifies the development of algorithms because we can use this fact. We will see how a global snapshot algorithm uses this result.There exists a sequence of steps in ascending epochs where the sequence is a computation. So there is a computation in which all steps with epoch \(t\) occur after all steps with epoch less than \(t\) and before all steps with epoch greater than \(t\). This fact simplifies the design of algorithms because we can work with a computation that executes steps sequentially in ascending order of epoch. We will see how we use the idea of increasing order of epochs in the consensus algorithm, Paxos.
Next
Logical clocks are used to record global snapshots as described here.K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology