A Global Snapshot Algorithm
A global snapshot algorithm records a state that can occur during a computation. The state obtained by the algorithm is called a global snapshot. Systems are monitored by taking repeated global snapshots. When a transient error is detected, a rollback and recovery algorithm restarts the computation from the most recent snapshot instead of starting it from the initial state.
Global Snapshot
A state of the system is a tuple with an element of the tuple for each agent and each channel. In this page, we also call the state of a system a global state or a system state to distinguish it from states of agents and states of channels.
A global snapshot algorithm is an algorithm that records the
global state of a system.
An algorithm to record the global state of a system is not instantaneous
because the algorithm records the states of multiple agents and
channels.
A global snapshot algorithm starts in some state \(S_{init}\) and terminates
later at a state \(S_{fini}\).
A global snapshot is a state S* such that there exists a
computation that starts at \(S_{init}\), then visits
\(S^{*}\) and then visits \(S_{fini}\).
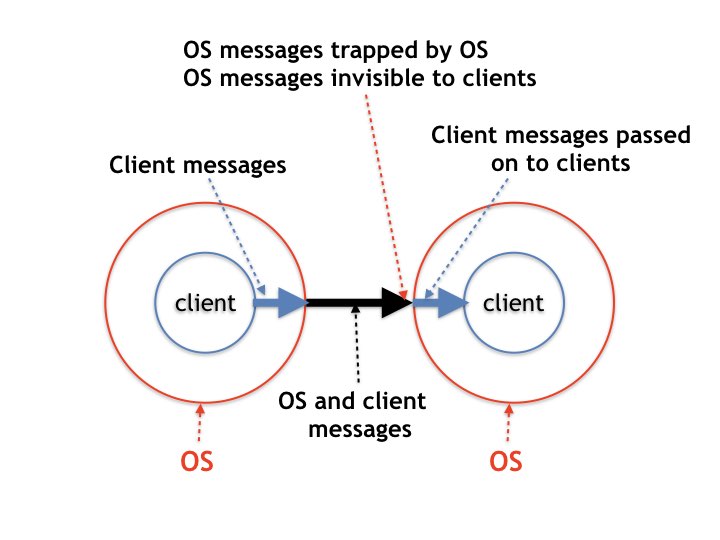
The global snapshot algorithm is an example of an algorithm that is executed by a distributed operating system (OS) on behalf of a client.
A Distributed Operating System
Each client agent has an OS agent that supervises it. OS agents use the same processors and channels as clients do. OS agents can record, but not modify, states of their clients. OS agents can send and receive OS messages that are not seen by clients.
Figure 1 is a representation of two OS agents that manage their client agents. Messages sent by a client are recorded by the OS and passed through to destination clients. The OS sends messages on the same channels as clients, but the OS traps these messages so that the client does not see them.
Execution of an OS agent on a processor may delay a client's steps on the same processor, and thus change the order in which the client's steps are executed. The OS may change a client's computation -- the order of steps -- but the OS must not change the client's dataflow.
One way to record a global snapshot is for the OS to stop a client computation, then take a global snapshot, and then restart the client computation. Our goal is to design an algorithm that does not stop the client.
Hereafter, when we refer to an agent in this webpage we mean an OS agent. Likewise, by messages we mean those that are sent and received by the OS.
Specification of a Global Snapshot Algorithm
Let \(S_{init}\) and \(S_{fini}\) be the states in which the global snapshot algorithm starts and finishes, respectively. The problem is to design a global snapshot algorithm that records a state \(S^{*}\) such that there exists a computation that starts at \(S_{init}\), then visits \(S^{*}\) and then visits \(S_{fini}\).
How Should You Solve the Problem?
Strategy
A straightforward strategy is as follows. Each agent logs its own computation -- the steps that the agent takes. Agents send their logs to an OS agent that stitches the logs together to get the dataflow of the computation. The agent then determines a consistent cut of the dataflow.
The strategy of sending agent logs to an agent for further analysis is a general strategy for developing algorithms that detect some property of a computation. More efficient strategies can be obtained for specific applications.
Our problem is: Develop an algorithm to determine the state at a consistent cut without requiring agents to log their steps.
A strategy for developing algorithms dealing with states that occur during a computation is to use properties of consistent cuts. The theorem "Computations and Cuts," tells us that \(S^{*}\) can be the state at any consistent cut. Our tasks reduce to (1) identifying a consistent cut, and (2) recording the state, \(S^{*}\), at the cut.
Identifying a Cut
Each agent has to record its own state because an agent's state is not
accessible to other agents.
The state of an agent v recorded by
v is called a local snapshot of v.
A partition of the steps of a computation into past and
future is a consistent cut (past, future) exactly when
all edges to vertices in past are from vertices in
past.
In our algorithm, let past be the set of steps at each
agent v before v takes its local snapshot.
To prove that the cut is consistent we need only prove that all
messages to steps in past are from steps
in past.
And this condition is guaranteed by the following rule.
Global Snapshot Rule
Each message received before the receiver takes its local snapshot is sent before the sender takes its local snapshot.
We now use the global snapshot rule to develop an algorithm.
The Global Snapshot Algorithm
A special OS message called a marker is used to distinguish
pre-snapshot from post-snapshot messages.
Messages sent on a channel before a marker is sent on the
channel are messages sent in the past -- i.e. before the
sender takes its local snapshot -- and messages sent
after the marker are sent in the future.
Steps of the global snapshot algorithm
- The algorithm begins by one or more agents taking their local snapshots. Any number of agents can initiate the global snapshot algorithm.
- When an agent takes its local snapshot it sends a marker on each of its outgoing channels. An agent takes its local snapshot exactly once. For each channel, exactly one marker is sent on the channel.
- When an agent receives a marker, the agent takes its local snapshot if it has not already done so.
- The snapshot of a channel is the sequence of messages received on the channel after the receiver takes its local snapshot and before the receiver receives a marker on the channel.
Proof of correctness
We will prove that the algorithm satisfies the global snapshot
rule: If an agent v received a message
m on a channel (u, v) before
v took its local snapshot then agent u
sent m before u took its local
snapshot.
Assume that agent v received a message
m on a channel (u, v) before
v took its local snapshot.
We will prove that agent u
sent m before u took its local
snapshot.
From rule 3, v takes its local snapshot when it
receives its first marker (which may arrive on any channel).
So, v received m before v
received the marker on channel (u, v).
Channels are first in first out.
Because v received m before v
received the marker on channel (u, v), it follows
that u sent m before u
sent the marker on channel (u, v).
From rule 2, u sent the marker on channel (u,
v) when u took its local snapshot.
So u sent m before u took
its local snapshot.
Proof about States of Channels
The messages in a channel at the cut are the
messages sent in past and received in future.
These are messages sent before the sender takes its snapshot and
received after the receiver takes its snapshot.
So, the state of a channel is the sequence of
messages received along the channel after the receiver takes its
snapshot and before the receiver receives a marker along the channel.
Note: If an agent takes its local snapshot when it receives a marker along a channel, then the snapshot of the channel is the empty sequence of messages.
Termination of the Algorithm
After any agent \(v\) initiates the algorithm, all agents that are reachable from \(v\) will receive a marker and take their local snapshots. If every agent is reachable from an initiator then all agents take local snapshots.
Each agent takes its local snapshot at most once. So, a marker is sent on a channel at most once. The computation terminates when all markers are received.
Next
Next, strategies for developing algorithms that use global snapshots and examples of applications of global snapshots and cuts.
A code skeleton of the algorithm and examples of the global snapshot algorithm are provided here.
K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology