Detailed Example: Earliest Meeting Time
We first consider a specific example and then generalize it. Three agents - Maya, Liu, and Eve - want to find a day at which all of them can meet. Associated with each agent \(j\) is a function \(f_{j}\) where \(f_{j}(d)\) is the earliest day at or after day \(d\) that agent \(j\) can meet.For example, assume that Maya, Liu and Eve are agents \(0\), \(1\), and \(2\), respectively. Maya, Liu and Eve can only meet on days that are multiples of 2, 3, 5, respectively (but none can meet on day 0). For example, \(f_{0}(5) = 6\) because the earliest time that Maya can meet on or after day 5 is day 6, because she cannot meet on day 5 since 5 is not a multiple of 2, and she can meet on day 6. Here are some examples of values of \(f_{j}(d)\):
\(
f_{0}(5) = 6, \; f_{0}(6) = 6, \; f_{0}(7) = 8
\)
\(
f_{1}(5) = 6, \; f_{1}(6) = 6, \; f_{1}(7) = 9
\)
\(
f_{2}(5) = 5, \; f_{2}(6) = 10, \; f_{2}(7) = 10
\)
In the example, the earliest day that Maya, Liu and Eve can all meet is the least common multiple of 2, 3, and 5 which is 30.
The function \(f_{j}\) is private to agent \(j\). An agent doesn't know the function of other agents. There exists some day, perhaps in the distant future, at which all agents can meet, and that day is \(m\). Therefore:
-
All agents can meet on day \(m\).
\( \forall j: f_{j}(m) = m \) -
For every day \(d\) before \(m\), at least one agent cannot meet
at \(t\).
\( \forall d < m: \exists j: f_{j}(d) > d \)
Associated with agent \(j\) is a variable \(t_{j}\). Let \(N\) be the number of agents, and let \(t\) be the vector whose elements are \(t_{j}\). Let \(M\) and \(\emptyset\) be vectors of length \(N\) where all elements of \(M\) are \(m\) and all elements of \(\emptyset\) are \(0\). In our example, \(t = [t_{0}, t_{1}, t_{2}]\), \(M = [30, 30, 30]\), and \(\emptyset = [0, 0, 0]\).
Specification
The specification of the system is as follows. The system is modeled as a do-od loop.Initially \(t = \emptyset\). Execution of the loop must terminate, and \(t = M\) at termination.
The Agent Graph
In this example, Maya and Liu communicate with Eve, but not with each other. The agent graph is shown below. The system has three agents - Maya, Liu and Eve - and shared variables \(t_{0}\), \(t_{1}\) and \(t_{2}\).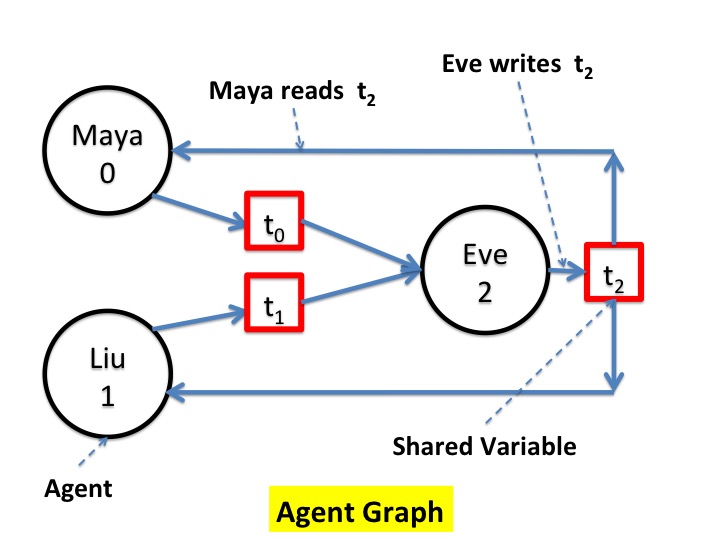 >
>
Eve's proposed meeting time, \(t_{2}\), is written by Eve and read by Maya and Liu. Likewise \(t_{0}\) is written by Maya and read by Eve, and \(t_{1}\) is written by Liu and read by Eve.
General Case
In the general case the agent graph has an arbitrary number of agents. The agent graph is strongly connected, i.e. there exists a path from every vertex to every other vertex.Agent's Algorithm
This problem has many algorithms. We give an example algorithm that illustrates how agent states appear in timeline diagrams. Each agent \(j\) writes variable \(t_{j}\). For every edge \((i, j)\) in the graph, agent \(j\) reads variable \(t_{i}\).Agent's Input/Output Operations
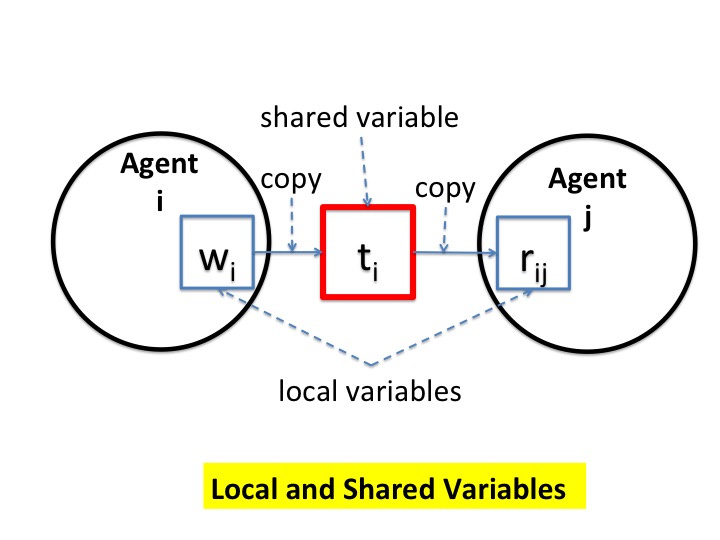
There are many types of shared variables. The type we use most often in this course is a message-passing channel. In this example, we look at a simple type of shared variable.Agent \(j\) has a local variable \(w_{j}\), and a local variable \(r_{i, j}\) for every edge \((i, j)\), where the symbols \(r\) and \(w\) stand for read and write, respectively. These variables are 0 initially. Agent \(j\) copies shared variable \(t_{i}\) into local variable \(r_{i, j}\), and it copies local variable \(w_{j}\) into shared variable \(t_{j}\). The guarded commands for these operations are:
\( \textbf{if} \; r_{i, j} \neq t_{i} \; \textbf{then} \; r_{i, j} = t_{i} \)
\( \textbf{if} \; t_{j} \neq w_{j} \; \textbf{then} \; t_{j} = w_{j} \)
We postpone discussion of how these operation that interface between
local and shared variables are implemented. Propose a couple of
implementations using multiple concurrent threads or a single
loop of execution.
 >
>
Note that with this input/output structure, values can get lost. For example, suppose \(w_{j}\) is 0 and then 1. Agent \(j\) may write 1 into shared variable \(t_{j}\) before agent \(k\) copies value 0 into its local variable \(r_{j, k}\).
When the shared variable is a queue of messages, the action of copying values between local and shared variables reduces to copying only the sequence of uncopied messages. We will discuss shared variable types later.
Local Step of an Agent
Agent \(j\) executes the following step:\( \textbf{if} \; t_{j} < f_{j}(\textrm{max}_{i} r_{i,j}) \; \textbf{then} \; t_{j} = f_{j}(\textrm{max}_{i} r_{i,j}) \)
The guarded commands of the system consists of the commands that copy values between local and shared variables, and the local steps of agents. Any command whose guard is true may be executed at each step. Only one command is executed at a time. However, you can see that two commands can be executed in either order if neither command modifies a variable that is referenced by the other. Execution in either order is a proxy for concurrent execution.
Later we will discuss methods by which all agents operate concurrently, and use protocols to ensure that a variable that is modified in one command is not referenced at the same time by another command.
The State Transition Graph
The graph is too large to fit conveniently into this module. The state of the system is a tuple containing the state of each agent and the state of each shared variable. The state of agent \(j\) is given by the values of \(r_{i,j}\) and \(w_{j}\), and the state of shared variable \(t_{j}\) is its value.The Timeline
An example of a partial timeline, only for agents 0 and 1, is shown in the figure below. The timelines for agents are in blue and timelines for shared variables in red. An internal event is the execution of a command that only references local variables of an agent, and that does not reference shared variables.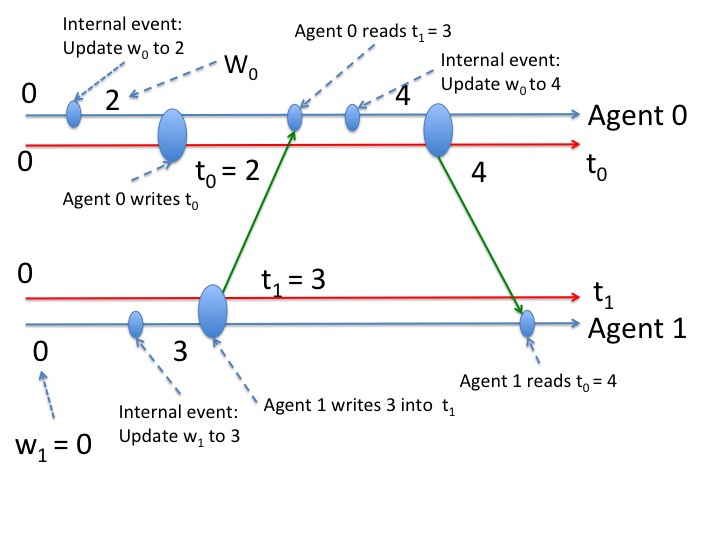
Proof of Correctness
The proof of correctness of a loop hinges on finding an invariant and a variant function. We use a variant function to prove that execution of a loop terminates. At termination, we use an invariant coupled with all guards being false to prove the desired property. You can find several examples of invariants and variant functions. Here is one example.Let \(S\) be a tuple which has an element for each shared variable \(t_{j}\), and local variables \(r_{i,j}\) and \(w_{j}\), for all \(i, j\). Let \(M\) be a tuple, of the same size as \(S\), where all the elements of \(M\) are the earliest meeting time \(m\). Let \(\emptyset\) be a tuple, of the same size as \(S\), where all the elements of \(emptyset\) are \(0\). We compare tuples lexicographically.
Invariant
It is straightforward to prove the following is an invariant.\( \emptyset \leq S \leq M \)
The invariant says that no local or shared variable overshoots the earliest meeting time \(m\), and they remain nonnegative.
Variant Function
Recall from the module on proving loop termination, we can use a variant function \(f\) and an invariant \(I\) in the following way. We prove that execution of a loop terminates by proving:\( \forall K: \quad (f=K) \wedge I \wedge (\exists j: g_{j}) \quad \rightarrow \quad f < K \)
An example of a variant function is \(M-S\). Its values are tuples of integers, and the invariant implies that it is bounded below by \(\emptyset\). We leave it to you to prove the above formula with \(f = M - S\). It is easy to see that the execution of any command with a true guard increases \(S\), and therefore decreases \(M-S\).
Practicalities
The model executes one action at a time. Actions that can be executed in arbitrary order represent actions that can be executed concurrently. A set of actions can execute concurrently provided that no action in the set modifies variables that are accessed by other actions in the set. We must ensure that an agent does not access a variable that is being modified by another agent by using locks or message-passing. We will discuss variables shared by agents in the next two sections.
K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology