Distributed Algorithms Contents Index

States: Examples

A Simple Example

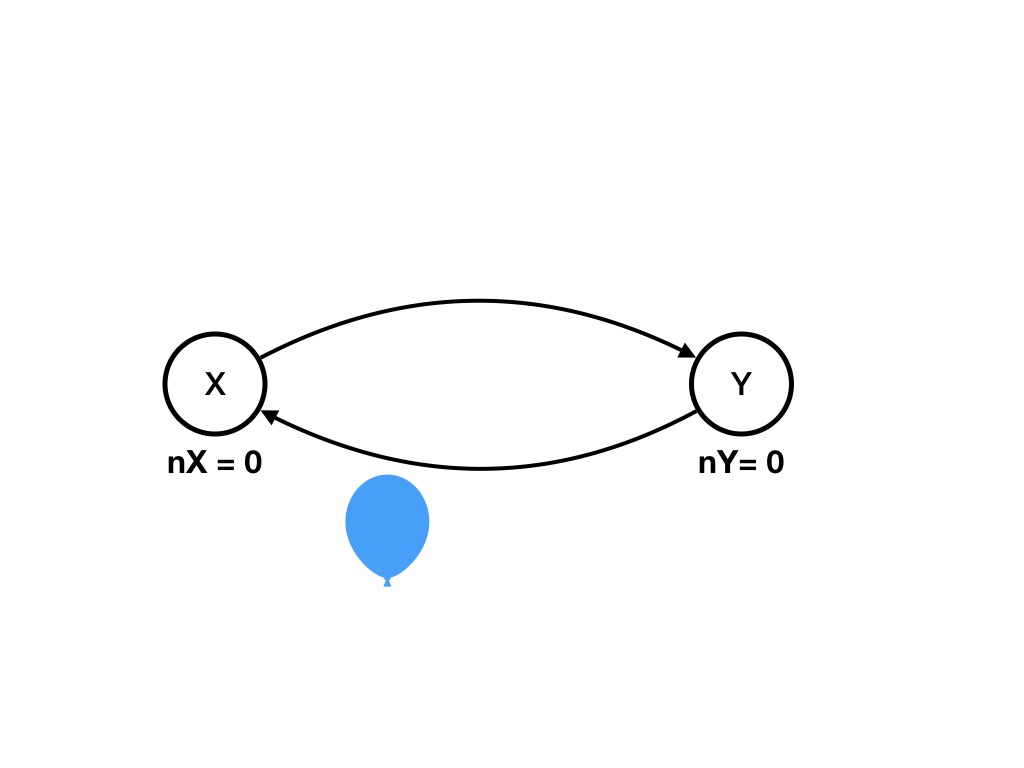
Two children, X and Y, are tossing balloons to each other. A balloon that has been tossed by X, while in the air to Y, is a message in the channel (X, Y). When a child gets a balloon it tosses the balloon back immediately. Initially there is a balloon tossed by X on its way to Y and there is also a balloon tossed by Y on its way to X.

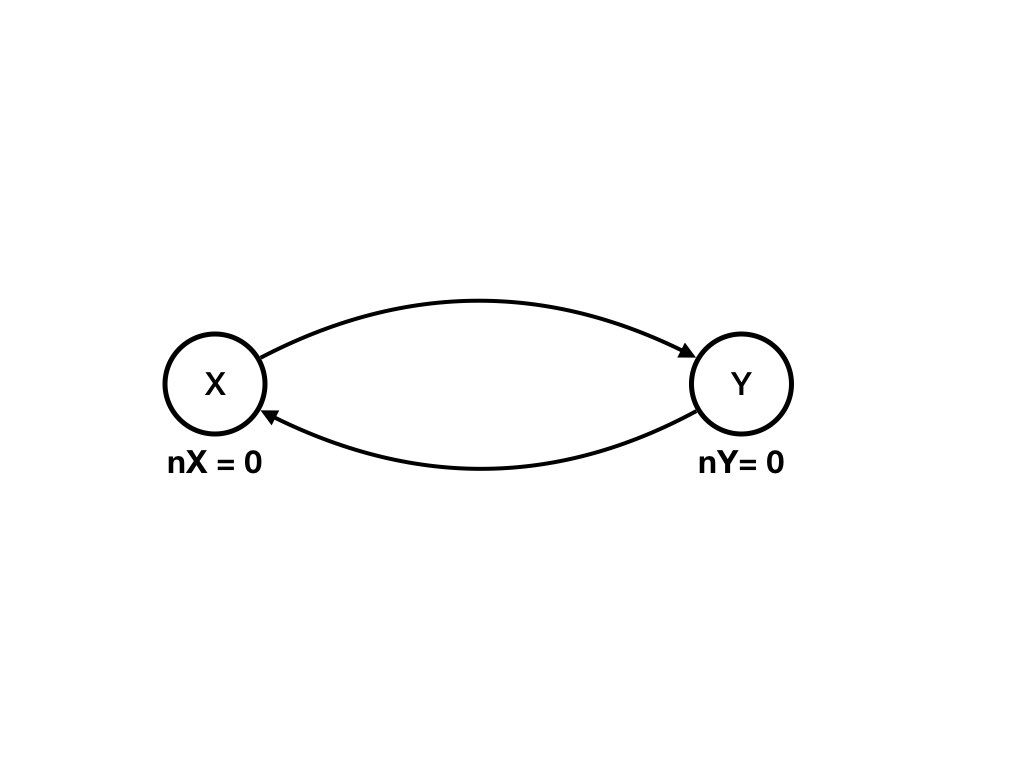
Each child has a countdown of the number of times it tosses balloons. Each time a child tosses a balloon it decrements its countdown value. After a child's countdown reaches 0 the child pops balloons that it receives (and doesn't toss popped balloons). Let nX and nY be the countdown values of X and Y, respectively.

Fig1
Figure State 1: Initial State
Fig2
Figure State 2. Y receives balloon. nY becomes 1
Fig3
Figure State 3. X receives balloon. nX becomes 0
Fig4
Figure State 4. Y receives balloon. nY becomes 0
Fig5
Figure State 5. X pops balloon. nX becomes 1
Fig6
Figure State 6. X pops balloon. nX becomes 0

Question

How is the state specified for this system?
Answer
The state of a channel is the number of balloons in it. The states of agent X and Y are the countdown values nX and nY, respectively.

For simplicity we will abuse notation and use (X, Y) to represent both the channel and the state of the channel, i.e., the number of messages in the channel. So the state of the system is the tuple: [nX, nY, (X, Y), (Y, X)].

Algorithm for X

# Initial State
nX = 1

# Callback function
def receive(message=m, sender=Y):
   if nX > 0:
      nX = nX - 1
      send(message=m, receiver=Y)
The algorithm for Y is identical except that initially nY = 2.

Question

A computation is specified as a sequence of states with a transition from each state to the next. What is the sequence of states corresponding to the diagrams: Figure State 1 to Figure State 6?

Answer

The sequence of states corresponding to the diagrams is as follows.

Initial State: Channel (X, Y) has one balloon and channel (Y, X) has one balloon. And the countdown for X is 2 and the countdown for Y is 3. We represent this state by:
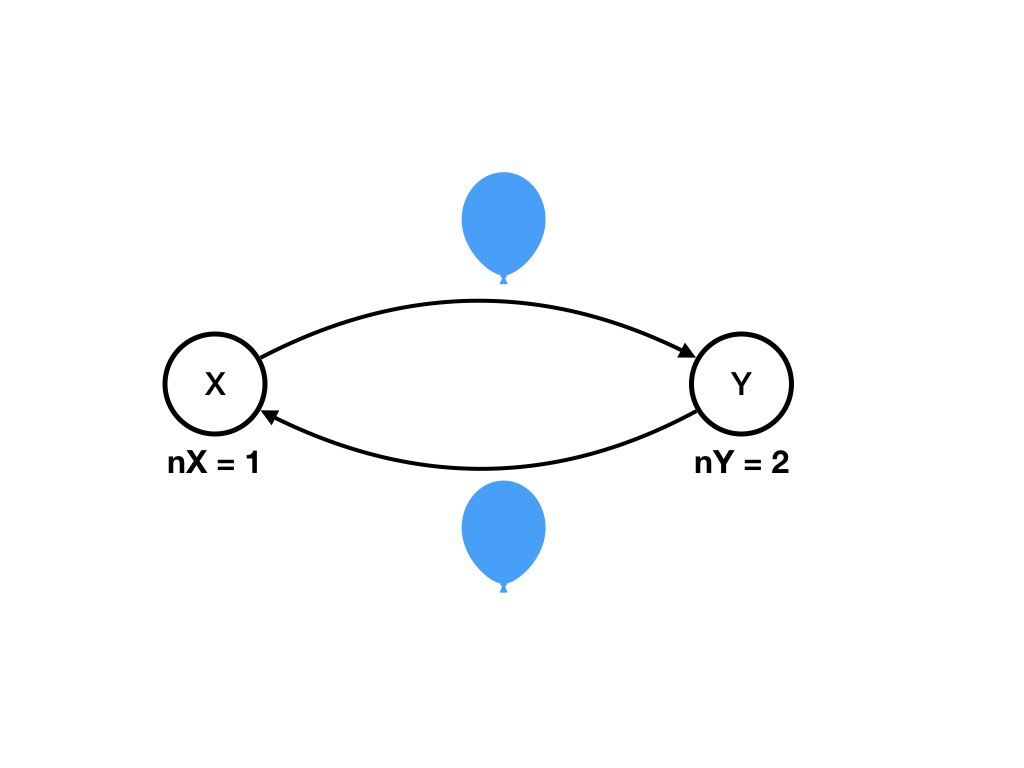
nX = 1, nY = 2, (X, Y) = 1, (Y, X) = 1

The sequence of steps from the initial state are as follows.

  1. Y receives a balloon and sends it back. So the state becomes:
    nX = 1, nY = 1, (X, Y) = 0, (Y, X) = 2
  2. X receives a balloon and sends it back. So the state becomes
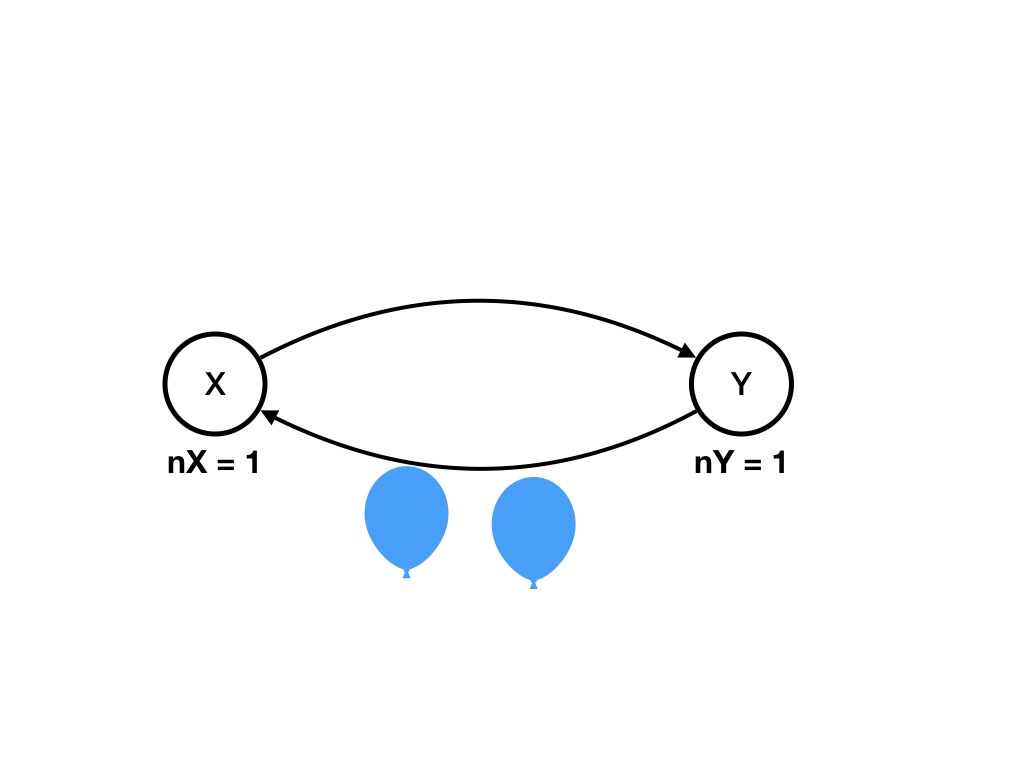
    nX = 0, nY = 1, (X, Y) = 1, (Y, X) = 1
  3. Y receives a balloon and sends it back. So the state becomes
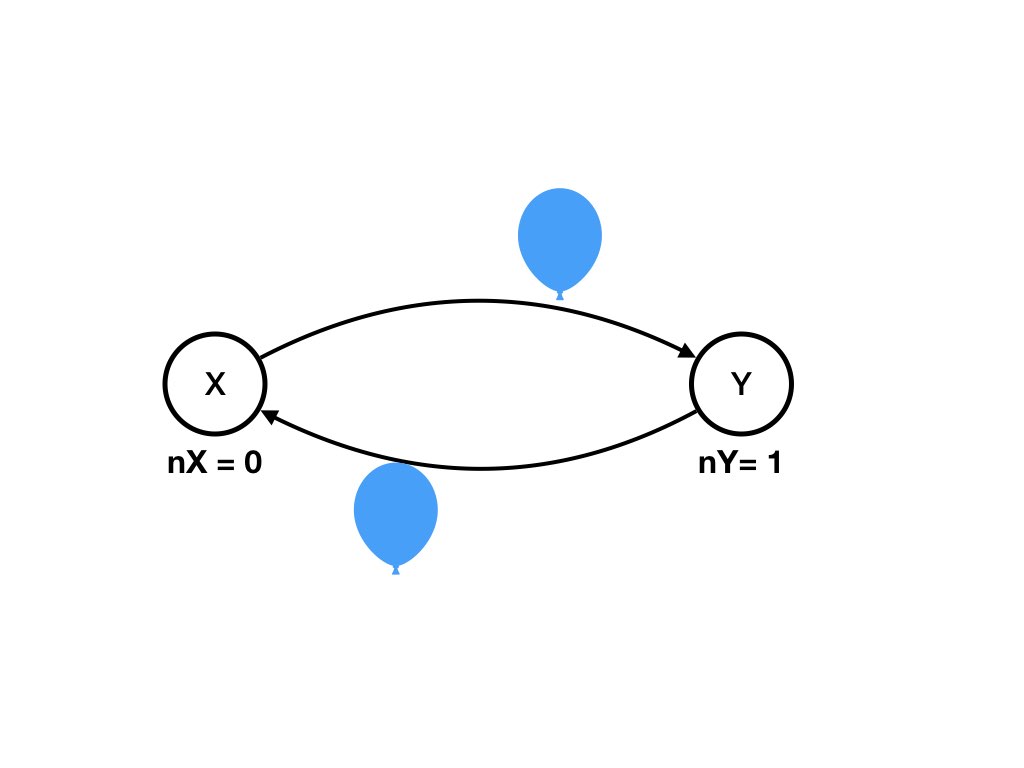
    nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 2
  4. X receives a balloon and pops it. So the state becomes
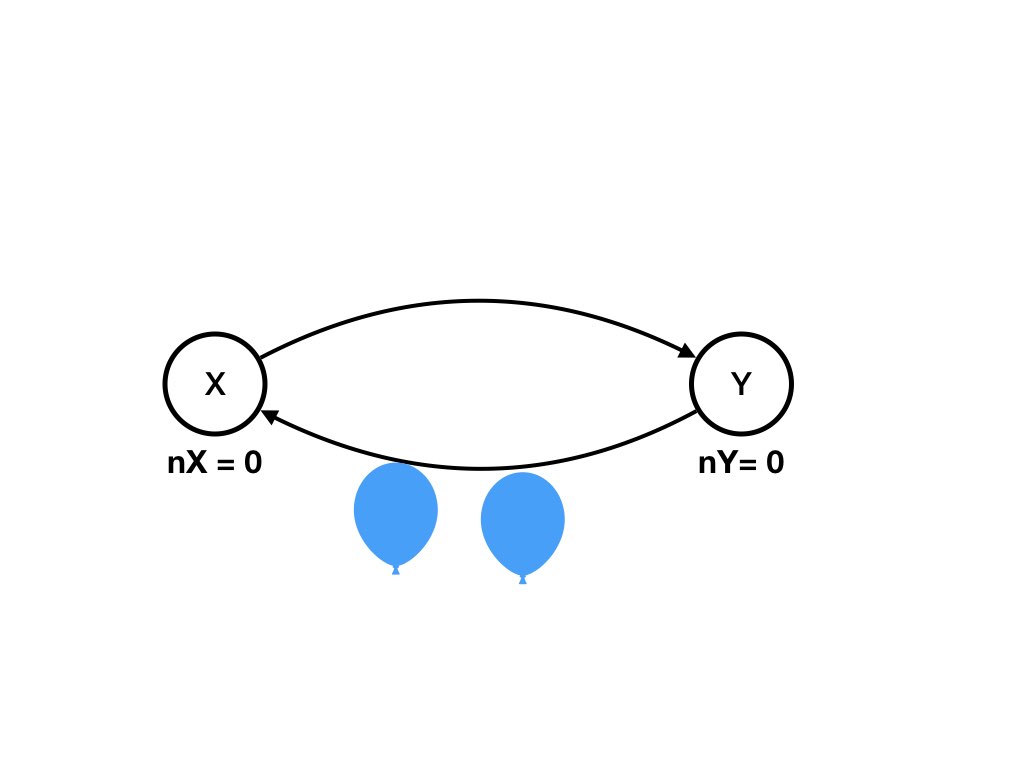
    nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 1
  5. X receives a balloon and pops it. So the state becomes
    nX = 0, nY = 0, (X, Y) = 0, (Y, X) = 0
There are no further steps in this computation.

Question

What is the event that causes the first state transition? This is the event in which Y receives a balloon for the first time.

Answer

Event: Y receives a balloon for the first time

This event is specified by the 4-tuple:
  1. Y's state before the event is nY = 2
  2. The message that is received is 1 (balloon) and the message is from X.
  3. Y's state after the event is nY = 1
  4. The message that is sent in the event is 1 (balloon) and the message is to X.

Question

Specify the state transition caused by the event in which Y receives a balloon for the first time.

Answer

The execution of this event at Y causes a state transition from
nX = 1, nY = 2, (X, Y) = 1, (Y, X) = 1
to
nX = 1, nY = 1, (X, Y) = 0, (Y, X) = 2

Question

In what states can the event in which Y receives the balloon for the first time be executed?

Answer

This event can be executed in any state S in which the inputs to the event are specified by the state, i.e., in S:

  1. Y's state in S is nY = 2
  2. The channel (X, Y) has a message 1 at its head.

Question

Specify the event in which X receives a balloon for the first time.

Answer

This event is specified by the 4-tuple:
  1. X's state before the event is nX = 1
  2. The message that is received is 1 (balloon) and the message is from Y.
  3. X's state after the event is nX = 0
  4. The message that is sent in the event is 1 (balloon) and the message is to Y.

Question

What is the state transition caused by the event in which X receives a balloon for the first time?

Answer

The execution of this event at X causes a state transition from
nX = 1, nY = 1, (X, Y) = 0, (Y, X) = 2
to
nX = 0, nY = 1, (X, Y) = 1, (Y, X) = 1

Example from Previous Pages

Question about State Transitions
What transitions are possible from the state shown in the following diagram from the example given earlier?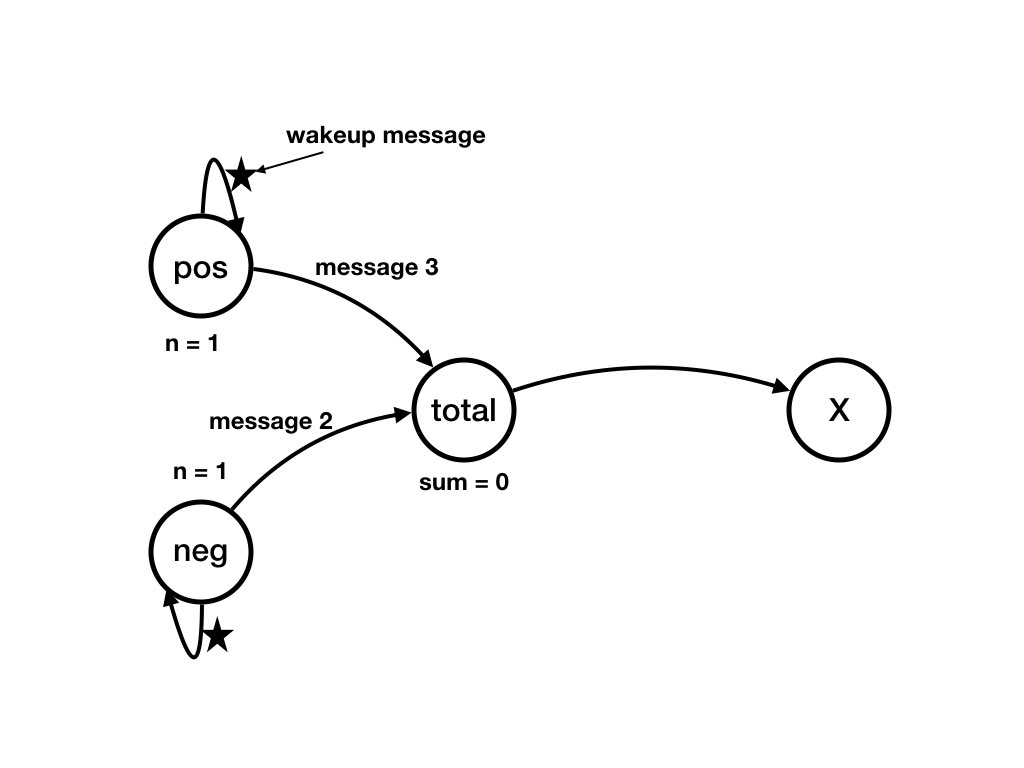
Fig1
Figure State S_0
There are four transitions possible corresponding to the four non-empty channels. The transitions from state S_0 are to states S_1, S_2, S_3, S_4 shown below in Figure State S_1, Figure State S_2, Figure State S_3, and Figure State S_4, respectively. They are shown in the following diagrams.
Fig2
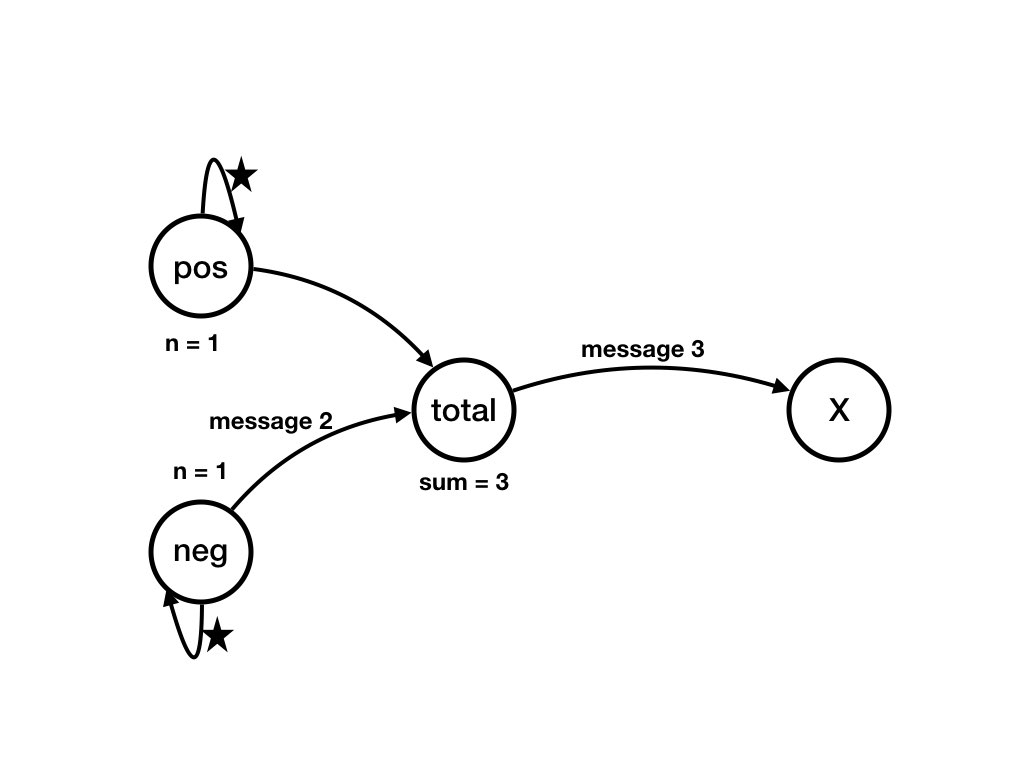
Figure State S_1: event total receives 3 from pos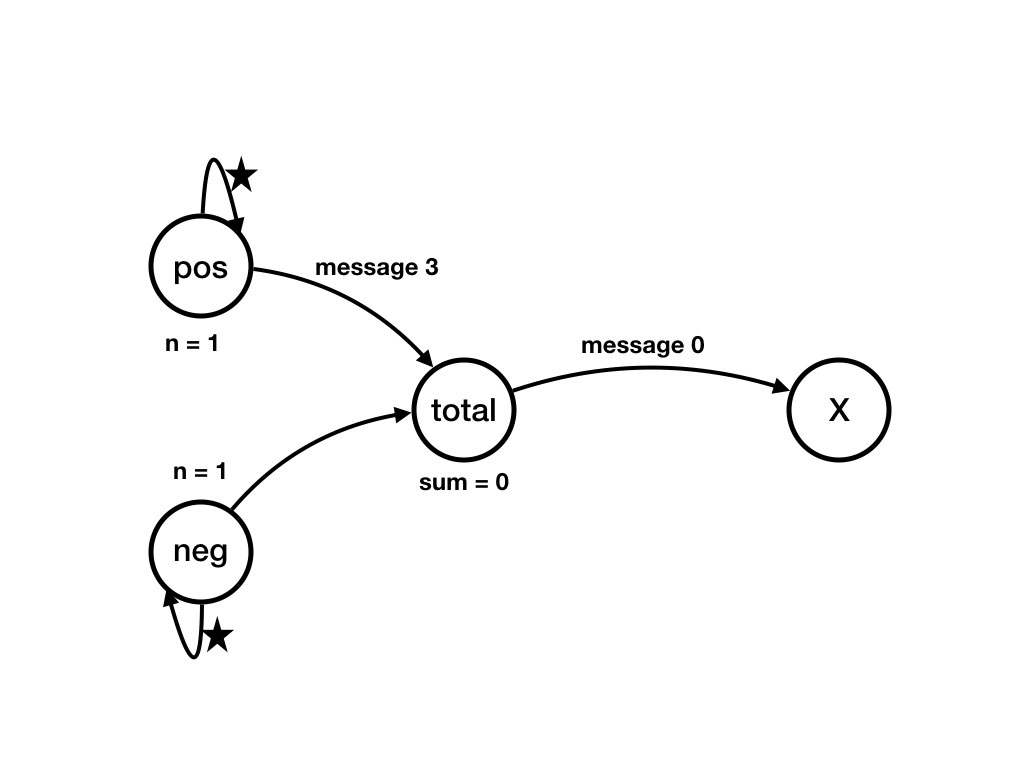
Fig3
Figure State S_2: event total receives 2 from neg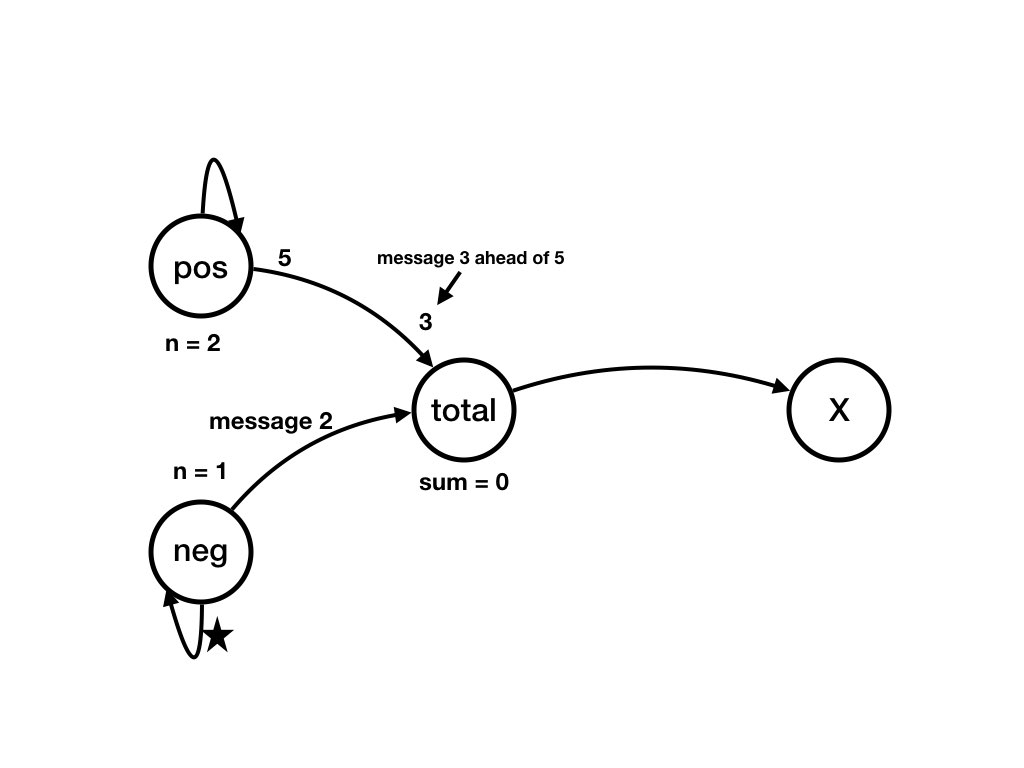
Fig6
Figure State S_3: event pos receives wakeup from pos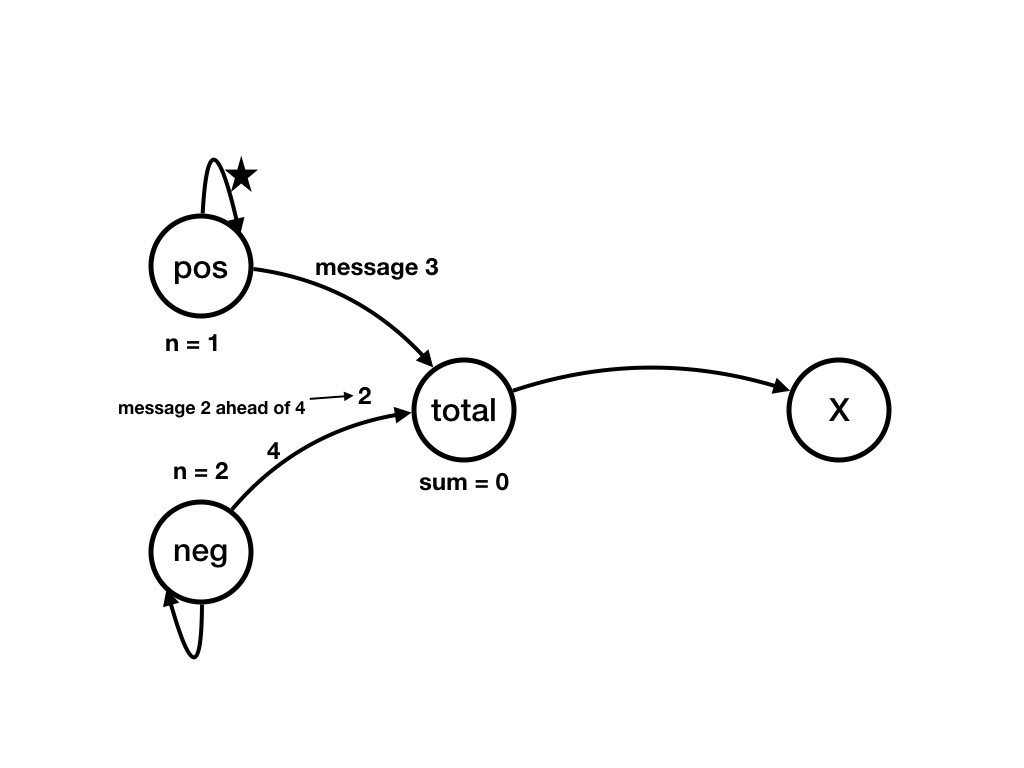
Fig7
Figure State S_4: event neg receives wakeup from neg
Next
Computations of a Distributed System.

Review material for this page

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology