Distributed Algorithms Contents Index

Detecting Database Deadlocks

A database deadlock occurs when each agent in a cycle remains waiting forever for a resource held and required by the next agent in the cycle. A database deadlock detection algorithm is executed by the operating system to determine whether there exists a cycle of deadlocked agents.

The Problem

The problem described here is a simplification of the database deadlock problem. The simplification captures the essentials of deadlock detection but ignores aspects of databases.

Agents in a system share a set of indivisible resources. An example of such a resource is exclusive access to a file. A deadlock arises when there is a cycle of agents, \([x_{0}, x_{1}, \ldots, x_{n-1}, x_{0}]\) where for all \(i\): Agent \(x_{i}\) is waiting to acquire resource \(r_{(i+1)}\) while agent \(x_{i}\) holds on to resource \(r_{i}\). Agent \(x_{i}\) has to hold resources \(r_{i}\) and \(r_{(i+1)}\) to continue executing. Operations on indices of agents are taken mod \(n\) and \(n > 1\).

Example

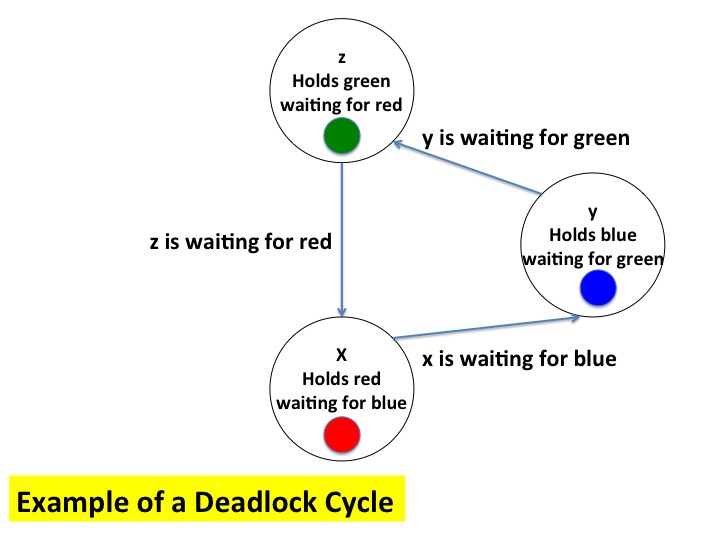
In the example, a resource is identified by its color. A system has one red, one blue, and one green resource. Agents \(x\), \(y\) and \(z\) are deadlocked in the following state.

  1. Agent \(x\) requires the red and blue resources to continue executing; \(x\) is holding the red resource and is waiting to acquire the blue resource.
  2. Agent \(y\) requires the blue and green resources to continue executing; \(y\) ; is holding the blue resource and is waiting to acquire the green resource.
  3. Agent \(z\) requires the green and red resources to continue executing; \(z\) holds the green resource and is waiting to acquire the red resource.
Fig2
Fig.1 - An Example of a Deadlock

How Should You Solve the Problem?

Strategy

Strategies for detecting stable properties are given here. Let's use the strategy of detection without observers.

The detection algorithm has two phases: (1) First a global snapshot algorithm is executed. (2) After the global snapshot algorithm terminates a distributed detection algorithm is executed on the local snapshots recorded by the global snapshots.

Algorithms for the second phase -- determining cycles are found here. The two phases can be merged for some problems, including this one.

A Distributed Algorithm to Detect a Cycle of Waiting Agents

Multiple detection algorithms and global snapshot algorithms may execute concurrently. These algorithms are disambiguated by tagging each algorithm with the initiator and a sequence id. Next we describe a single detection algorithm which is executed after a single global snapshot algorithm terminates.

Local Constants

In the detection algorithm, each agent v has the following local constants:
  1. v.waits is the set of resources that v has to acquire from other agents to start execution.
  2. v.holds is the set of resources that v holds and must continue to hold to start execution.

Example

In the example of the figure:
x.waits = {blue}, x.holds = {red}
y.waits = {green}, y.holds = {blue}
z.waits = {red}, y.holds = {green}

v.waits and v.holds are determined in the first phase of the detection algorithm in which agents take local snapshots. In the second phase v.waits and v.holds are constant.

Messages

Each message m sent by an agent v has a field m.waits where: m.waits = v.waits.

Initiating the Algorithm

A waiting agent u initiates the algorithm by sending a message m on each of its output channels where m.waits = u.waits.

Action by an Agent other than the Initiator

  1. If v has already sent messages then v takes no action.
  2. If v has not sent messages, and if there is a resource common to m.waits and v.holds then v sends a message m' on each of its output channels where m'.waits = v.waits.

Cycle Detection

If the initiator u receives a message m where there is a resource common to m.waits and u.holds then u detects a cycle of waiting agents.

Proof of Correctness

The proof outline is as follows. An agent v sends messages only if there is a path of waiting processes from u to v. So, u detects a cycle of waiting processes only if there exists a cycle of waiting processes.

If there exists a cycle of waiting processes from u to u then messages are sent along one such cycle, and so u detects a cycle.

The algorithm terminates because it sends at most one message on each channel.

Example

This example shows steps in the case of the cycle of waiting processes shown in figure 1. The algorithm is initiated by agent x by broadcasting a message m where m.waits = x.waits = {blue}.

When y receives a message m where m.waits = {blue}, there is a resource in both m.waits and y.holds, and so y broadcasts message m' where m'.waits = y.waits = {green}.

When z receives a message m where m.waits = {blue}, z takes no action because there is no resource in both m.waits and z.holds.

When z receives a message m where m.waits = {green}, z broadcasts message m' where m'.waits = z.waits = {red}.

When the initiator x receives a message m where m.waits = {red}, x detects a deadlock because there is a resource common to m.waits and x.holds.

Combining Cycle Detection and Snapshot Algorithms

We can use a a marker in the snapshot algorithm as a message in cycle detection. Modify a marker m to have the field m.waits used in cycle detection. Then the snapshot algorithm is essentially the same as the cycle detection algorithm.

Next

Next, chapter on consensus algorithms.

Frequently Asked Questions

Review

K. Mani Chandy, Emeritus Simon Ramo Professor, California Institute of Technology