Self Stabilization

This module describes one example of a self-stabilization system --- a system that recovers automatically from transient errors.

A self stabilizing system recovers automatically from transient errors. If a self-stabilizing system enters an unsafe state then the system will correct itself and eventually enter a safe state.

The literature on self stabilization is extensive. Let's look at one example of a self-stabilizing system to get an idea of its design.

Self Stabilizing Token Passing

A ring of agents passes a single token around the ring. An agent that holds the token knows that no other agent has the token at that point. So, the system can be used to implement mutual exclusion.

Examples of errors are the disappearance of the single token and the creation of additional tokens. A self stabilizing algorithm ensures that eventually the system gets back to a safe state, i.e., one in which it has exactly one token.

Let's begin with a model in which each agent in the ring can read the state of its predecessor in the ring. Later, we will modify the algorithm to work with message-passing.

\(N\) agents, indexed \(j\), are organized in a ring where agent \((j+1) \: \textrm{mod} \: N\) can read the state of agent \(j\). Hereafter, we will not write "\(\textrm{mod} \; N\);" it is to be understood.

An agent is either idle or active. The system is required to have exactly one active process. The active process can be thought of as having the single token in the system. The token is passed from agent \(j\) to agent \(j+1\) when agent \(j\) becomes idle and agent \(j+1\) becomes active.

For convenience in visualizing diagrams, let's assume that the state of an agent is a color. Next we describe the basic algorithm that assumes that errors do not occur; later we will modify the algorithm to obtain a self-stabilizing algorithm that recover from errors.

The Algorithm

The algorithm for agent \(0\) is different from that of the other agents. Agent \(0\) has the token exactly when its color is the same as that of its predecessor. Any other agent holds the token exactly when its color is different from that of its predecessor.

An agent \(j\) passes the token to agent \(j+1\) when agent \(j\) changes its color. Agent \(0\) has the token when all the agents in the ring have the same color.

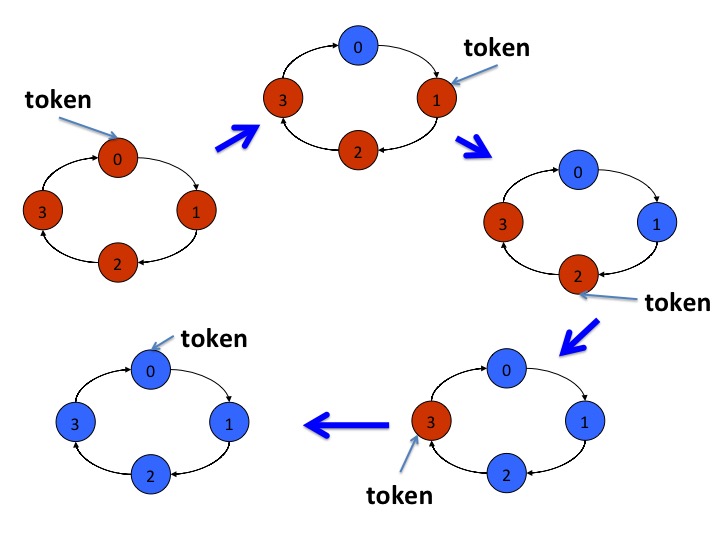
The diagram below illustrates an example with 4 agents where an agent's color is either red or blue. The diagram shows how the token is passed from each agent to its sucessor.

In the figure on the top left, all the agents are red; so agent 0 has the token. When agent 0 changes its color we get the diagram at the top center. In this diagram, agent 0 is blue and all the other agents are red. Agent 0 no longer has the token because its color is different from that of its predecessor; however agent 1 does have the token because its color is different from that of its predecessor. The sequence of diagrams shows what happens when the agent holding the token --- which is the only active agent --- changes its color.

Faults

Let's look at the state of a system after a fault occurs. The next set of diagrams shows how errors --- once they occur --- can propagate for ever. These diagrams show a system with three tokens whereas an error-free system should have exactly one. The three agents holding tokens are shown with large yellow numbers and the agent that does not hold a token is shown with a smaller black number.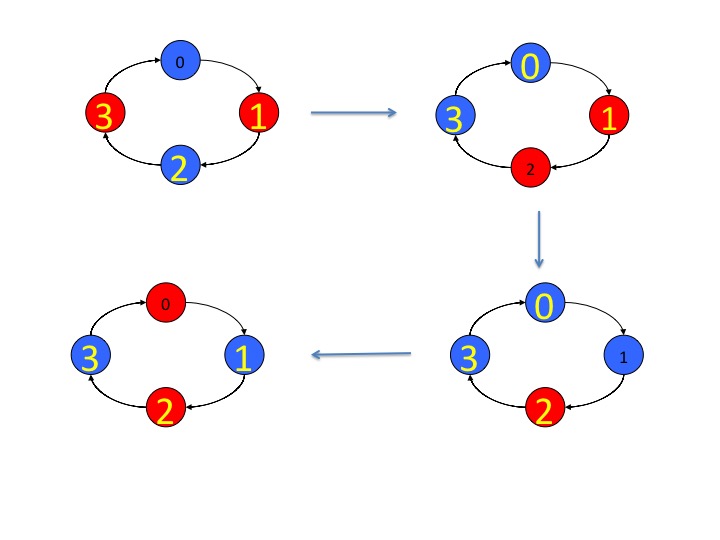

The figure on the top left of the above diagram shows agents 1, 2 and 3 with tokens because their colors are different from those of their predecessors. The next diagram, top right, shows agents 1 and 3 with tokens because their colors are different from those of their predecessors, and agent 0 with a token because its color is the same as that of its predecessor. The transition to the diagram on the top right from the one on the top left occurs when agent 3 changes its color.

The sequence of state transitions gets the system to the figure on the bottom left which is the same as that on the top left with the colors reversed. This cycle of state transitions can repeat forever, with the same system always having three tokens. So, this system is not self stabilizing.

A Self-Stabilizing Algorithm

The solution: add more colors!

We will modify the design to have as many colors as there are agents. In our example, we will have 4 colors because it has 4 agents. The algorithms for all agents, other than agent 0, remains unchanged. As before agent 0 has the token when its color is the same as that of its predecessor and agent 0 sends the token by changing agent 0's color. The difference in the self-stabilizing algorithm is the color to which agent 0 transits.

Assume that the 4 colors are numbered 0, 1, 2, 3. If agent 0's color is \(k\) it makes a transition by changing its color to \(k \: \textrm{mod} \: N\).

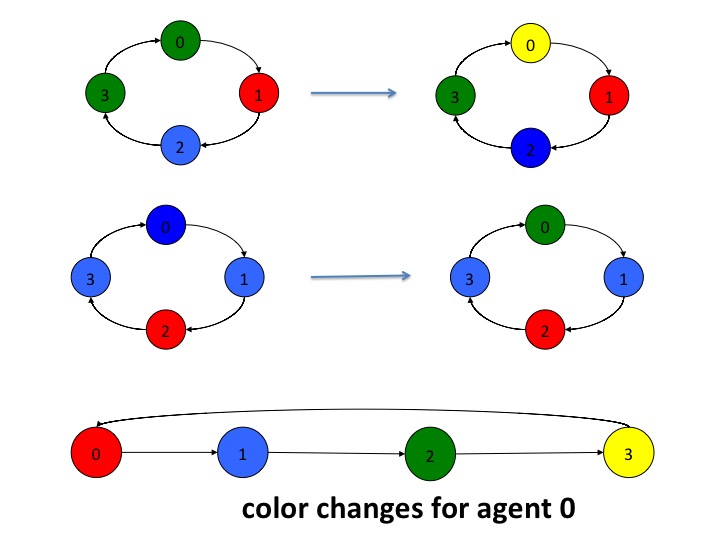
The diagram below gives an example of how agent 0's color changes. Its sequence of colors, 0, 1, 2, 3 are red, blue, green, yellow, respectively. The diagram on the top left shows a configuration in which agent 0 holds a token because its color (green --- number 2) is the same as that of its predecessor. Agent 0 passes the token by changing its color to 3 (yellow), as show on the diagram on the top right.

The diagram in the middle left shows agent 0 with a token. It passes the token by changing its color from 1 (blue) to 2 (green), as shown in the diagram in the middle right.

Proof

The proof has the following three ideas that we first describe informally.

1. In all states at least one agent holds a token.
2. All trajectories from all states lead to a state in which agent 0 holds a token.
3. A trajectory from a system state in which agent 0's color is different from that of the other agents leads to a state in which all agents have the same color (in which case the system is in a safe state).

Part 1

If all agents have the same color then agent 0 holds a token. If there is more than one color in the ring then there is at least one agent, other than agent 0, whose color is different from that of its predecessor's; so, that agent holds a token.

Part 2

Agent 0 and agent \(n-1\) will get the same color at some point because agent 0's color will propagate all the way around the ring unless it gets to agent \(n-1\) sooner.

Part 3

If agent 0's color is different from the colors of agents \(1, \ldots, n-1\) then the only trajectory that leads to agents 0 and agent \(n-1\) having the same color is for agent 0's color to propagate all the way around the ring.

The system always reaches a safe state

Let \(S\) be any state. Let the \(C\) be the set of agent colors in state \(S\). If \(C\) has all \(N\) colors, then the color of agent \(0\) is different from the colors of the other agents, and so the result follows from part 3.

If \(C\) has fewer than \(N\) colors then the color of each agent remains a color in \(C\) until agent 0 gets a color that is not in \(C\). At this point agent 0's color is different from that of the other agents and the result follows.

Review

1. In this algorithm, does any agent detect that the system is in an unsafe state? Can we determine that the system is in an unsafe state based solely on the state of any one agent and the state of its predecessor? Why?
2. Will this algorithm work if the number of colors is arbitrarily large, and more than the number of agents? Why?
3. Will this algorithm work if the number of colors is less than the number of agents? Why?