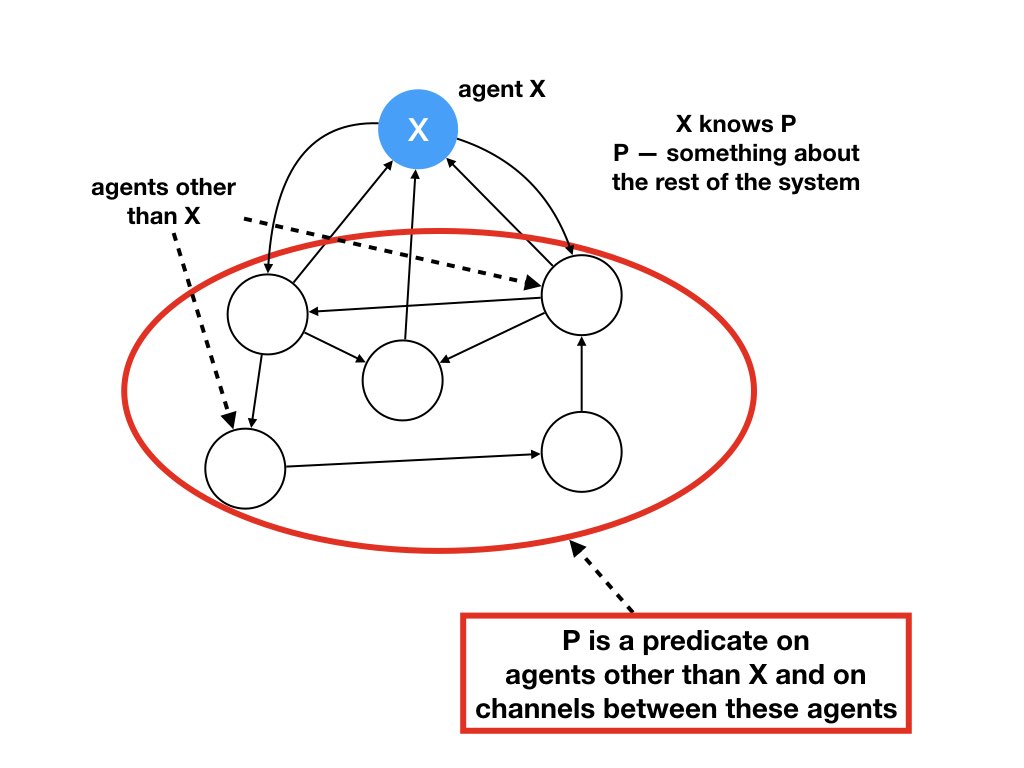
What Agents Know

Programmers often use phrases such as "this agent knows that the other agent is idle" or "in the algorithm the detector agent must learn that all channels are empty." This page gives a formal definition for the frequently used informal phrase: "An agent knows something about other agents and and channels."

Key Idea

We sometimes use anthropmorphic arguments in reasoning about systems --- we invest digital agents with human characteristics. For example, a programmer may say "an agent knows that another agent is idle." Endowing software with human capabilities can be dangerous when terms are ambiguous. This page defines the phrase "what an agent knows" and presents theorems about knowledge in distributed systems.

Predicates and Truth Sets

In this module we define a predicate "agent \(x\) knows \(P\)" where \(P\) is a predicate on states of a system.

The phrase "predicate \(P\) holds in state \(S\)" means that \(P(S)\) evaluates to True in state \(S\) of the system. Associated with each predicate \(P\) is the set of states in which \(P\) holds; this set is called "the truth set of the predicate."

When the domain of discourse is the set of all people, "is a student" is a predicate, and the truth set of this predicate is the subset of people who are students. For a predicate \(P\), the truth set of \(\neg P\), where \(\neg\) means NOT, is the complement of the truth set of \(P\).

For example, the truth set of \(P \wedge Q\) (where \(\wedge\) is boolean AND) is the intersection of the truth set of \(P\) and the truth set of \(Q\). Likewise, the truth set of \(P \vee Q\) (where \(\vee\) is boolean OR) is the union of the truth set of \(P\) and the truth set of \(Q\).

This module presents theorems about what agents know. We restrict attention to what a single agent knows about the states of other agents and the states of channels between the other agents. We can define what collections of agents know about other agents, but here we restrict attention to what a single agent knows. Also, we won't consider what an agent knows about itself or about channels incident on the agent itself. We study what an agent knows about the rest of the system.

What do Programmers mean by "Agent Knows?"

We begin with examples and an informal discussion of the phrase "what an agent knows." Later, we will define the phrase and give theorems about knowledge. The proofs are based on dataflow graphs.

Example: Four-Way Handshake

A system consists of a controller and a furnace. The furnace is in one of two states: the furnace is either on or the furnace is off. The controller sends messages to the furnace to turn the furnace off or on. The controller has four states S0, S1, S2, S3.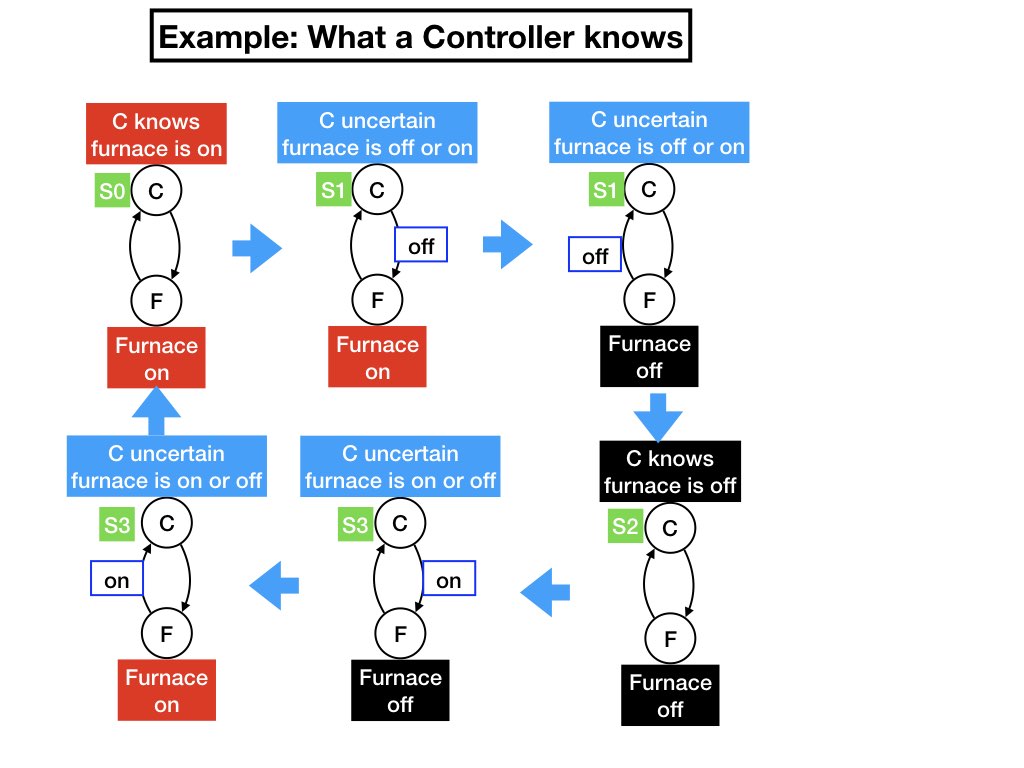

The controller is represented in the diagram by agent C, and the furnace by agent F. There are channels in both directions between the agents.

The diagram on the top left shows a system state in which the controller is in state S0, and the furnace is on, and both channels are empty. In state S0 the controller knows that the furnace is on. The controller makes a transition from S0 to S1 by sending a message "turn off" message to the furnace. (The controller receives a message from itself that causes the transition, and internal messages are not shown.)

The diagram in the middle of the top row shows a system state in which the controller is in state S1, the furnace is on, and there is a message "turn off" from the controller to the furnace, and the channel from the furnace to the controller is empty. In state S1 the controller doesn't know whether the furnace is off or on because the controller doesn't know whether the "turn off" message has reached the furnace.

When the "turn off" message reaches the furnace, the furnace turns off, and sends a message "furnace turned off" to the controller. The diagram on the right-hand side of the top row shows a system state in which the controller is in state S1, the furnace is off, there is a message "furnace turned off" from the furnace to the controller, and there is no message from the controller to the furnace.

When the controller receives the message that the furnace has been turned off the controller transits to state S2 in which it knows that the furnace is turned off. The diagram at the right-hand side of the bottom row shows a system state in which the controller is in state S2, the furnace is turned off, and both channels are empty.

The controller transits from state S2 to S3 when it sends a message to the furnace to turn on. When the controller is in state S3 it doesn't know whether the furnace is on or off. The diagram in the middle of the bottom row shows a state in which there is a turn-on message from the controller to the furnace, the controller is in state S3, the furnace is turned off, and there is no message from the furnace to the controller.

When the furnace receives the turn-on message the furnace turns itself on and sends a message to the controller "furnace turned on." The diagram at the left-hand side of the bottom row shows a system state in which the furnace is turned on, there is message from the furnace to the controller that the furnace is on, the controller is in state S3, and the channel from the controller to the furnace is empty.

When the controller receives the message that the furnace is on, the controller transits back to state S0 in which it knows that the furnace is turned on. The figure below shows the states and state transitions of the controller.

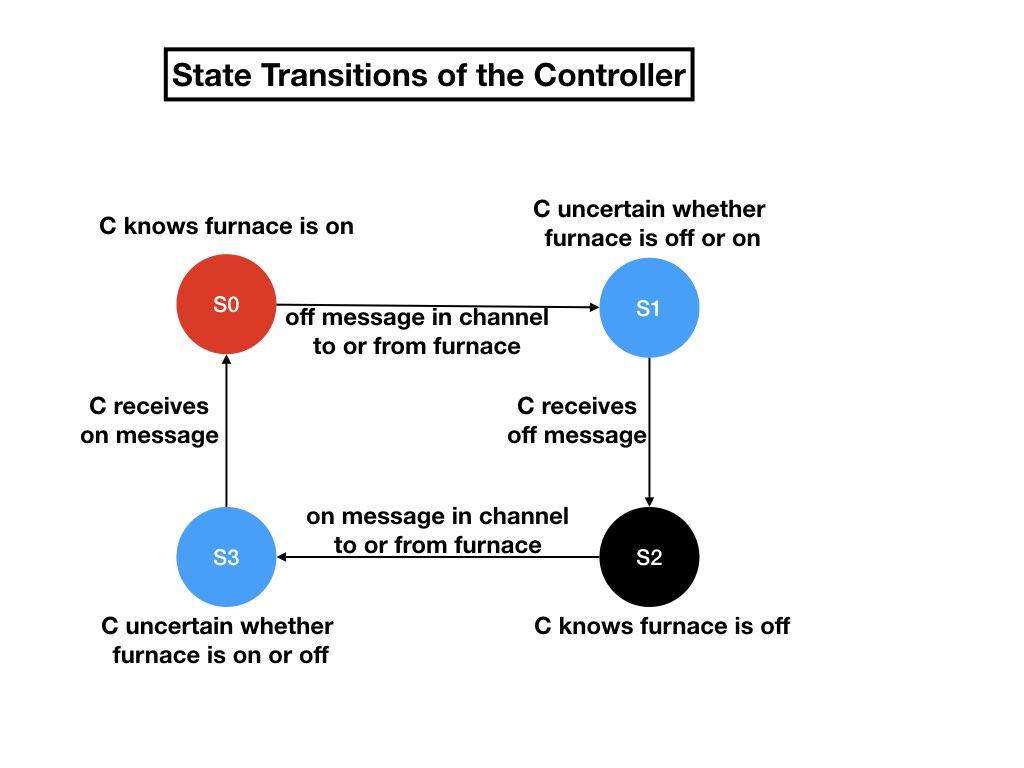
Here are a couple of questions to check your reading of the example: In what states does the controller know that both channels are empty? In what states does the controller know that the channel from the controller to the furnace contains a message?

The controller knows that both channels are empty in states S0 and S2. There is no state in which the controller knows that the channel from the controller to the furnace contains a message. The controller cannot know that the channel contains a message.

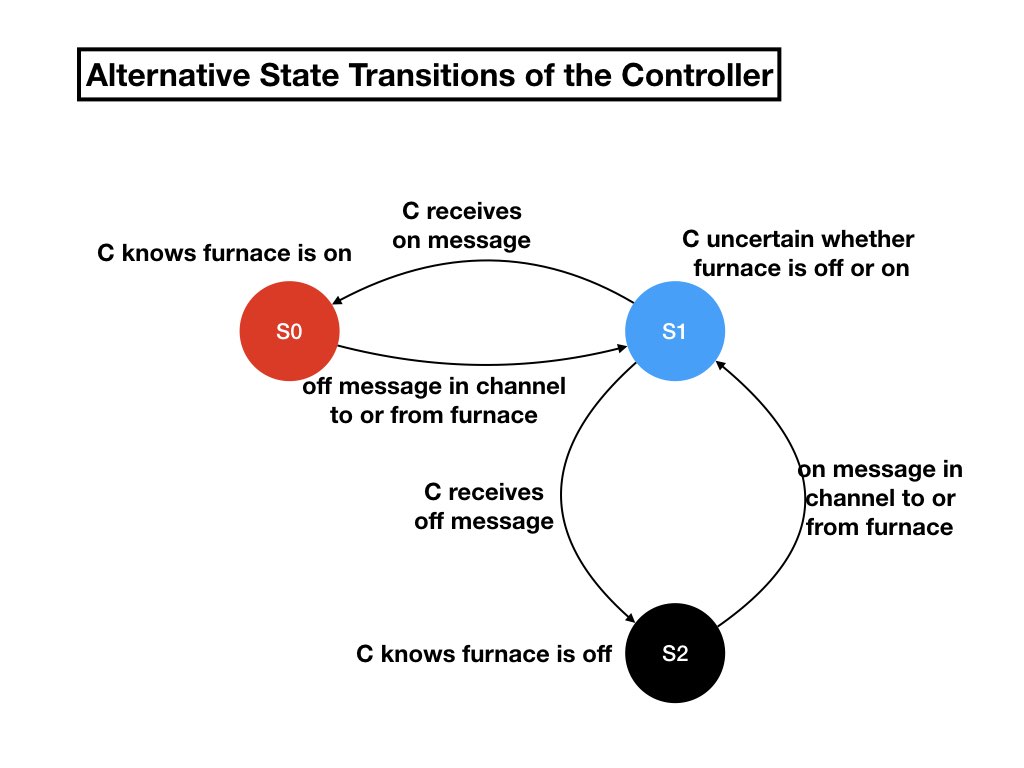
We will say that the controller is uncertain whether the furnace is off or on when controller doesn't know that the furnace is on and the controller also doesn't know that the furnace is off. We can combine the two states in which the controller is uncertain into a single state.

The 4-step sequence of messages between the two agents is called a "four-way handshake" in communication protocols and asynchronous circuit design.

Example: Step in which Agent sends no Messages to other Agents

Let's look at another example, see figure 4. The diagram on the left-hand side shows a system state in which (1) the controller (C) knows that the furnace is off and that the furnace temperature is less than 2000 degrees; (2) the furnace is off and its temperature is less than 1000 degrees; (3) there is a message from the furnace to the controller saying that the temperature has dropped to 1000; and (4) there is no message from the controller to the furnace.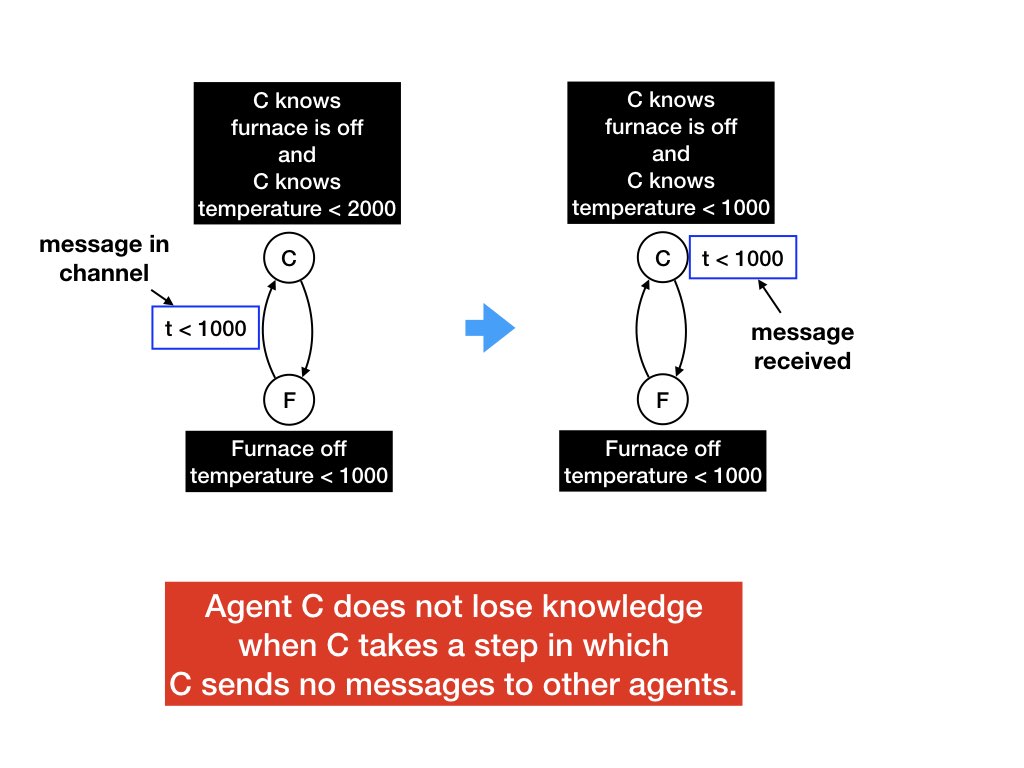

Let's look at the step in which the controller receives the message that the temperature has dropped to 1000 degrees. In this step the controller sends no messages to other agents. (The controller may send a message to itself, and self-messages aren't shown in the diagram.)

The knowledge that the controller had before it received the message -- i.e., the temperature is below 2000 -- is retained after the message is received. The controller now knows more, i.e., that the temperature is below 1000, but the controller does not lose the knowledge that it had before the message arrived. We will prove a theorem that an agent does not lose knowledge when it carries out a step in which it sends no messages. As we see an agent may gain knowledge when it receives messages.

Example: Step in which Agent receives no Messages from other Agents

Let's look at another example, see figure 6. In this example a controller (C) controls a furnace and a valve. In the diagram on the left-hand side the controller knows that the furnace is on and the valve is closed.

Let's look at a step of the controller in which the controller receives a message from itself (not shown in the diagram) and the controller sends a message "open valve" to the valve. The controller transitions to a state in which it knows that the furnace is on and is uncertain about whether the valve is open or closed.

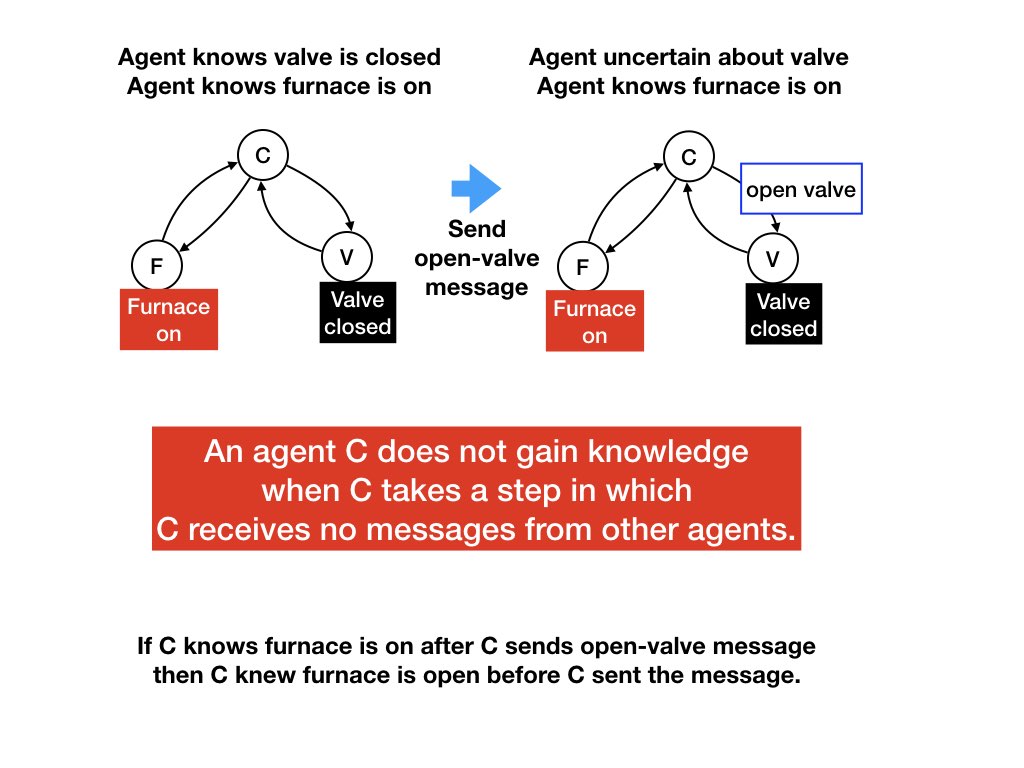
An agent can lose knowledge when it sends a message -- for example, the controller lost the knowledge that the valve is closed. An agent cannot gain knowledge in a step in which it sends messages but does not receive messages from other agents: If the agent knows that the furnace is on after it sent the message then the agent knew that the furnace was on before it sent the message.

Example: What an Agent Doesn't Know

A programmer may use a phrase such as "agent X doesn't know that agent Y is idle when X is active." She probably means:

NOT (X knows Y is idle) when X is active.

She probably does not mean: X knows Y is NOT idle holds when X is active.

For any agent X and predicate P on states of channels and states of agents other than X:

if "X knows NOT P" then NOT ("X knows P").

We saw in the examples that there may be states of X in which X is uncertain about P; these are states in which NOT ("X knows P") and also NOT("X knows NOT P").

Next, let's give a formal structure to our intuitive understanding.

What an Agent Knows: Theory

Recall that a system state is a tuple with an element of the tuple for each agent and each channel in the system. Let \(S_{x}\) be the state of agent \(x\) when the system state is \(S\).

Let \(x\) be an agent and let \(P\) be a predicate. "\(x\) knows \(P\)" is a predicate on the states of agent \(x\).

\(x\) knows \(P\) holds in a state \(s\) of agent \(x\) exactly when for all states \(S\) of all computations that start from an initial state:

---

if \(S_{x} = s\) then \(P\) holds in \(S\).

---

When we use the phrase "X knows P" we restrict attention to predicates P on states of agents other than X itself and on channels between agents other than X. We are concerned with what X knows about other parts of the system.

Example

In figure 1, the controller is agent C, and let P be the predicate "furnace is on". The predicate P holds in the three system states marked "furnace is on" in the figure. P holds in all system states in which C is in state S0. Therefore C knows P when C is in state S0.

Does C know P when C is in state S1? When C is in state S1 the system state may be either the state shown in the diagram in the middle or the right of the top row of figure 1. P does not hold in one of the system states. Therefore C knows P is false when C is in state S1.

Example

This example shows a system with two agents, X and Y, and channels in both directions between them. The system has two tokens. A token is either in a channel or held by an agent. The diagram shows some (but not all) of the system states.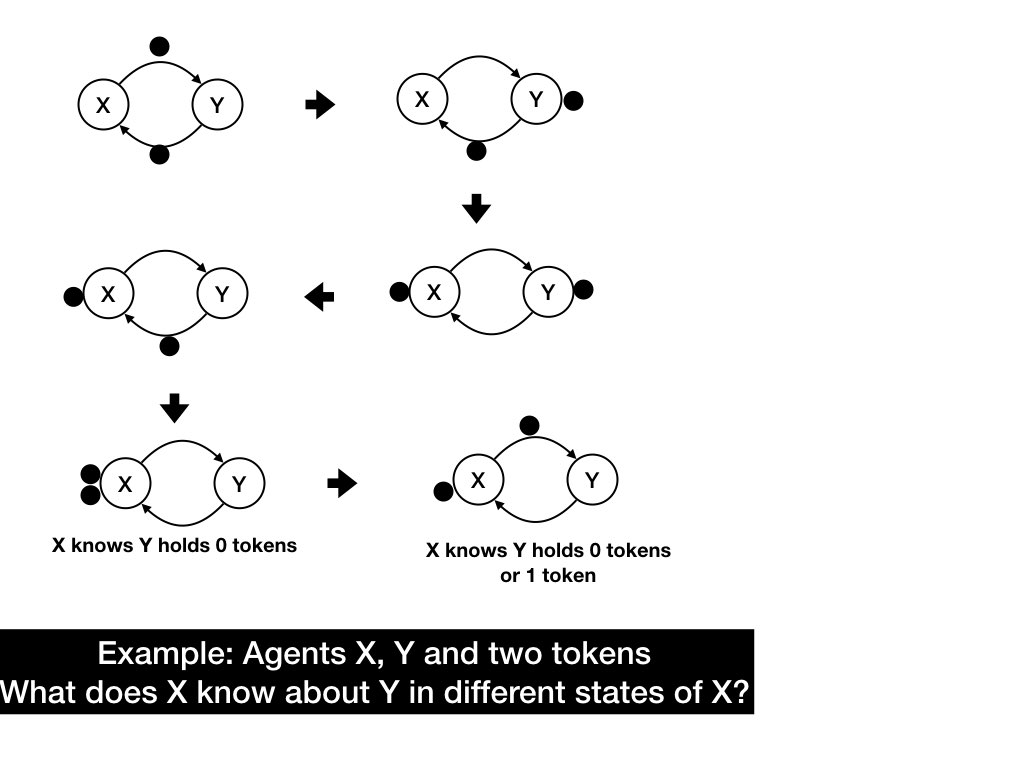

The set of system states in which X holds both tokens consists of the single state shown in the left-hand side of the bottom row in which Y holds no tokens. Therefore, X knows that Y holds no tokens when X holds both tokens.

In what states of X does X know that Y holds 0 or 1 tokens? The system states in which X holds 1 token has the other token in a channel (in which case Y holds 0 tokens) or is held by Y. Likewise, when X holds both tokens, Y holds 0 tokens. So, X knows that Y holds at most 1 token exactly when X holds at least one token.

In what states does X know that Y holds one token? There is no state of X in which X knows that Y holds one token. This is because if X holds 0 tokens or 1 token then the other tokens may be in channels and so Y may hold no token.

X cannot know that Y holds a token. i.e.,

NOT("X knows Y holds a token")

Example

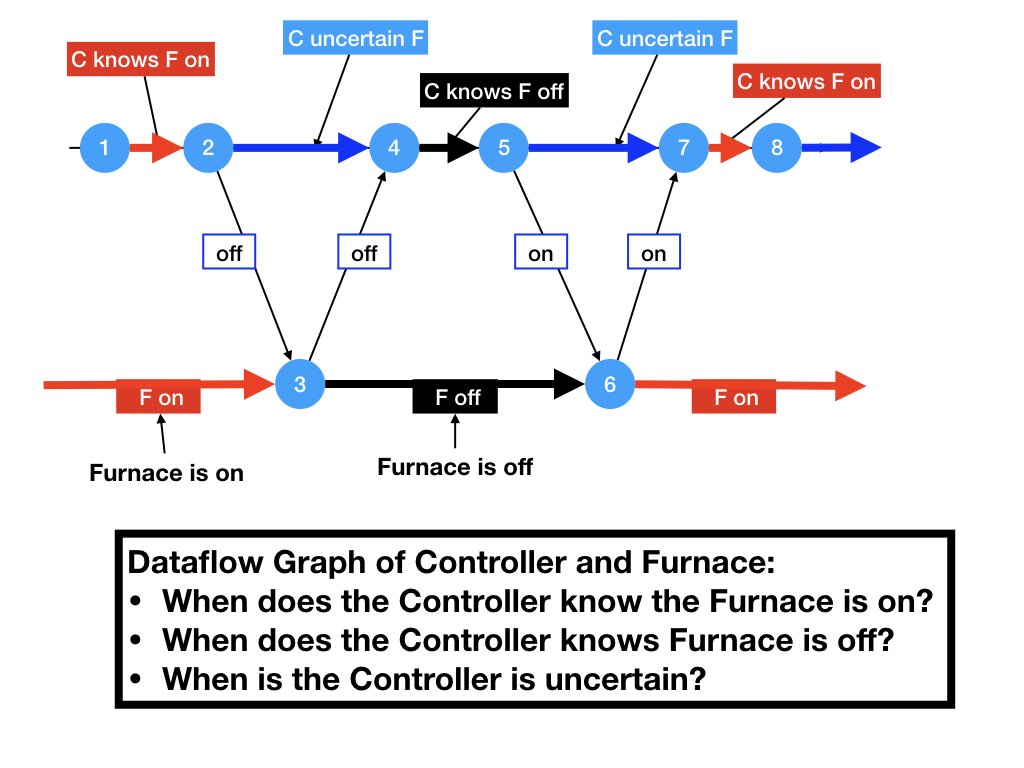
Figure 8 shows the dataflow graph of the example illustrated by figure 1. The top horizontal line of the dataflow graph has steps of the controller C, and the lower line has steps of the furnace F.

The controller knows that the furnace is on between steps 1 and 2. The controller sends the turn-off message in step 2, and the message is received by the furnace in step 3. When the furnace receives the message it turns the furnace off and sends a message that the furnace is off. The controller receives the message in step 4.

What the controller knows about the state of the furnace at different steps in the computation is shown in the figure. The controller knows that the furnace is on, then is uncertain, then knows that the furnace is off, then is uncertain, and then knows again that the furnace is off.

Agent Knowledge and Dataflow

A point in a computation of an agent \(x\) in a dataflow graph is an edge \((e, e')\) between steps \(e\) and \(e'\) at \(x\), and the state of \(x\) at the point is given by the label of the edge.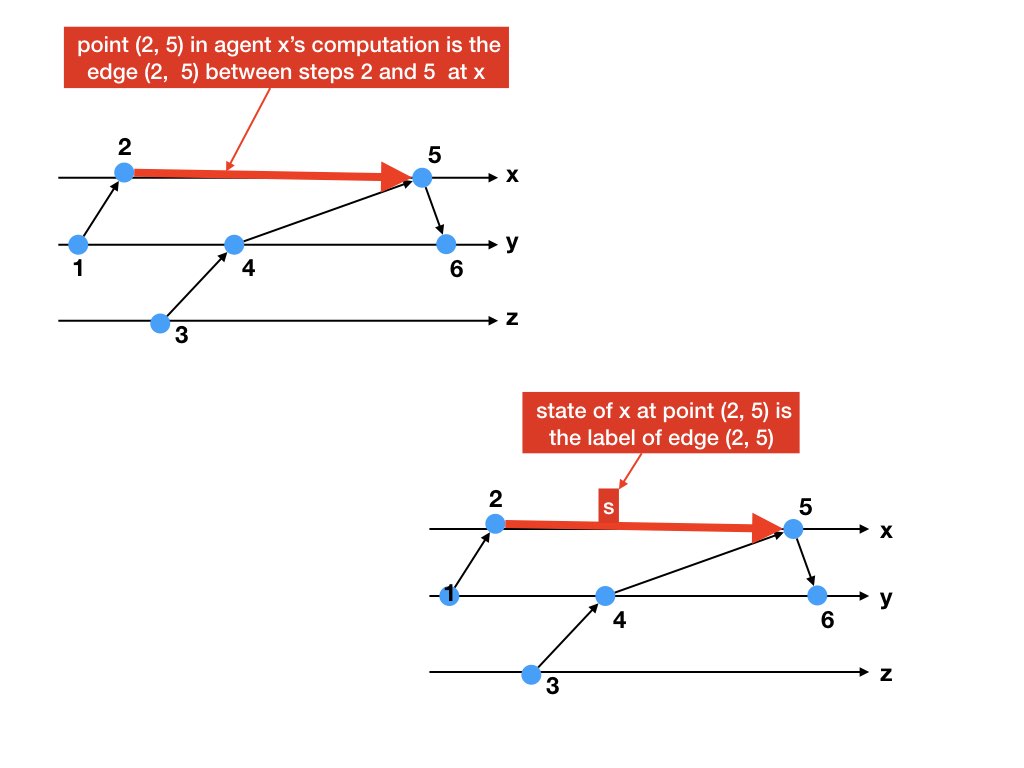

"\(x\) knows \(P\) at point \((e, e')\) in \(x\)'s computation in a dataflow graph" means that \(x\) knows \(P\) when \(x\) is in the state at point \((e, e')\) in the graph.

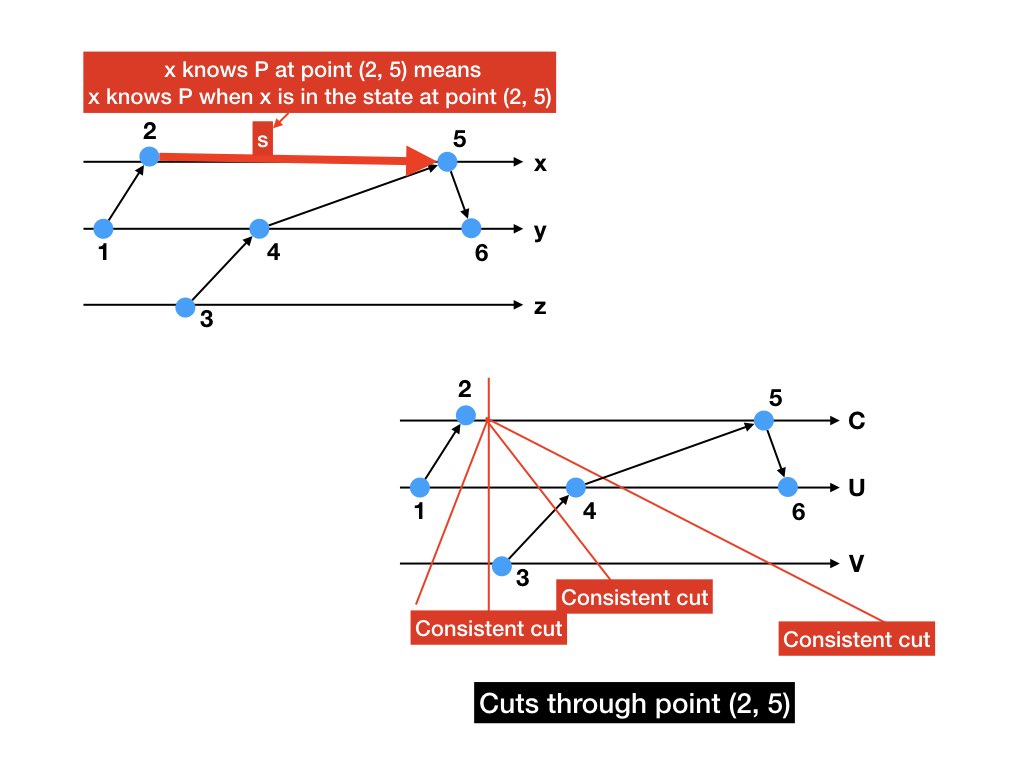
A cut through a point \((e, e')\) in \(x\)'s computation is a partition (past, future) where \(e\) is in past and \(e'\) is in future. We say that a predicate \(P\) holds at a consistent cut (past, future) exactly when \(P\) holds at the state at the cut.

Lemma about Consistent Cuts

If \(x\) knows \(P\) at a point in \(x\)'s computation then \(P\) holds in the states of all consistent cuts through that point.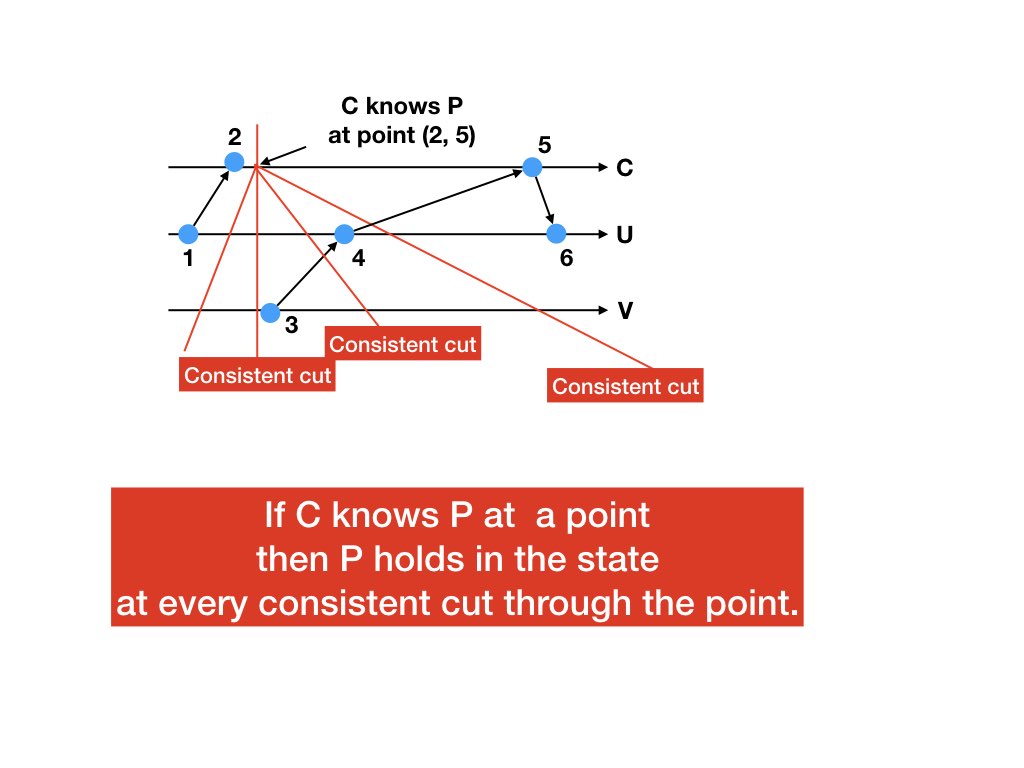

Proof

Assume \(x\) knows \(P\) at a point \((e, e')\) in a system computation. Let the state of \(x\) at the point be \(s*\). Then \(x\) knows \(P\) holds in state \(s*\).

Let \(S\) be the state of a consistent cut through the point, and let \(S_{x}\) be the state of \(x\) in system state \(S\). Then \(S_{x} = s*\).

Because \(x\) knows \(P\) when \(x\) is in state \(s*\), and \(S_{x} = s*\) it follows that \(P\) holds in \(S\).

An Agent Can Lose Knowledge Only When It Sends a Message to Another Agent

Theorem

Let \(e, e', e''\) be successive steps at an agent \(C\) in a computation. If \(C\) knows predicate \(P\) at point \((e, e')\) in the dataflow graph of the computation, and if \(C\) sends no messages to other agents in step \(e'\), then \(C\) also knows \(P\) at point \((e', e'')\).

Example

The figure shows a part of a dataflow graph of a computation with steps 1, 2,..7 and agents C, U, V. Steps 2, 5, and 7 are at agent C; steps 1, 4 and 6 are at agent U; and step 3 is at agent V. The message sent in step 4 by U is received in step 5 by C.

Let P be a predicate on the states of U, V and the channels between U, V. The theorem says that if "C knows P" holds at point (2, 5), i.e., after step 2 and before step 5, then "C knows P" holds at point (5, 7), i.e. after step 5 and before step 7.

Proof of Theorem

Let \(s*\) be \(C\)'s state at point \((e', e'')\). We will show that \(P\) holds in all states \(S\) in all computations that start in an initial state, where the state \(S_{C}\) of agent \(C\) is \(s*\) when the the system state is \(S\).

Consider the dataflow graph of any computation that starts in an initial state. Let \(e, e', e''\) be successive steps at an agent \(C\) in a computation, where \(C\) knows predicate \(P\) at point \((e, e')\). We will show that \(P\) holds in all states at consistent cuts through the point \((e', e'')\).

Let (past, future) be any consistent cut through \((e', e'')\). Let past* be the set of steps identical to past except that \(e'\) is not in past*. There is no edge from \(e'\) to steps in past, and therefore the cut (past*, future*) is consistent.

The cut (past*, future*) passes through edge \((e, e')\). \(C\) knows \(P\) at point \((e, e')\) and therefore \(P\) holds at the cut (past*, future*).

The event of all agents other than \(C\) are the same in past and past*. Because \(P\) holds at cut (past*, future*) it follows that \(P\) also holds at cut (past, future). Therefore, \(P\) holds at all consistent cuts through point \((e', e'')\).

Example

Consider a consistent cut through point (5, 7) in the figure, such as the cut shown by the red dotted line. past at this cut is {1, 2, 3, 4, 5}, and past* is {1, 2, 3, 4}. It is obvious that all edges to past* are from past*. So, the cut specified by past* = {1, 2, 3, 4} is consistent. In the figure, the cut corresponding to the steps to the left of the black dotted line is consistent.

The states of agents U, V are the same after events {1, 2, 3, 4, 5} and events {1, 2, 3, 4} have been executed.

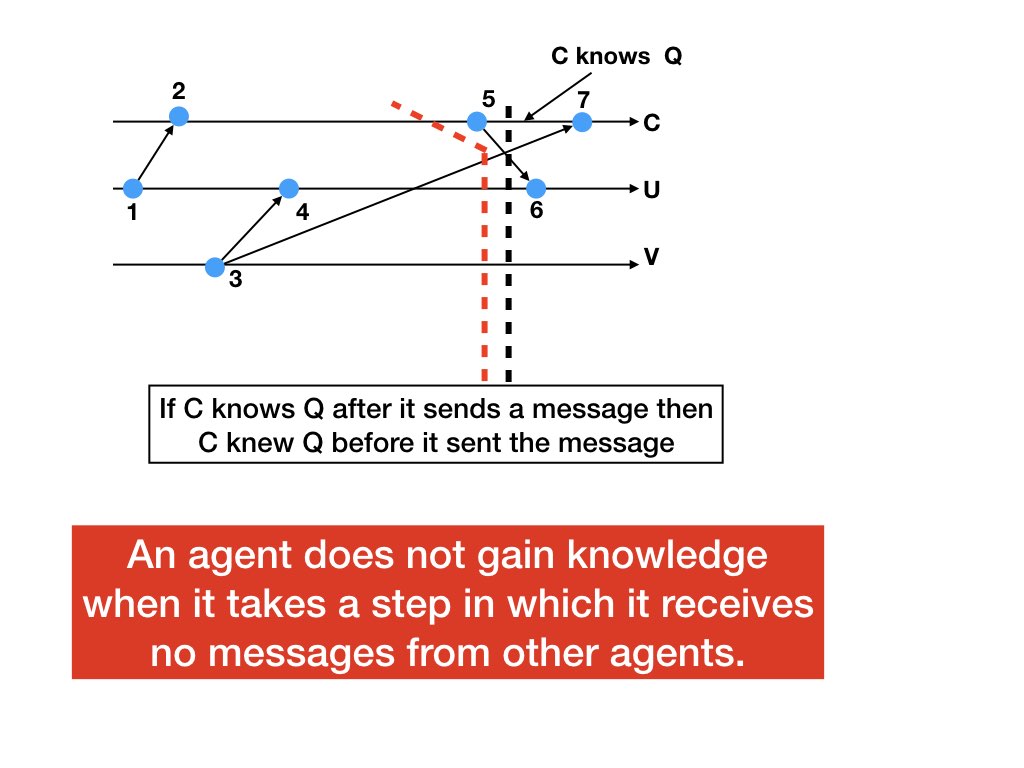
An Agent Can Gain Knowledge Only When It Receives a Message from Another Agent

Theorem

Let \(e, e', e''\) be successive steps at an agent \(C\) in a computation. If \(C\) knows predicate \(P\) at point \((e', e'')\) in the dataflow graph of the computation, and if \(C\) receives no messages from other agents in step \(e'\), then \(C\) also knows \(P\) at point \((e, e')\).

Proof

The proof uses dataflow graphs in the same way as in the proof of the previous theorem.

Example

In the figure below, the theorem says that if \(C\) knows \(P\) at point (5, 7) in the dataflow graph then \(C\) knows \(P\) at point (2, 5). Because \(C\) knows \(P\) at (5, 7) it follows that \(P\) holds at the cut shown by the vertical black dotted line in which past is {1, 2, 3, 4, 5}.

The cut {1, 2, 3, 4} is also consistent. The states of U, V are the same after events {1, 2, 3, 4} and {1, 2, 3, 4, 5} are executed. So, if \(P\) holds after {1, 2, 3, 4, 5} then it also holds after {1, 2, 3, 4}.

Theorem about Flow of Data to Gain Knowledge

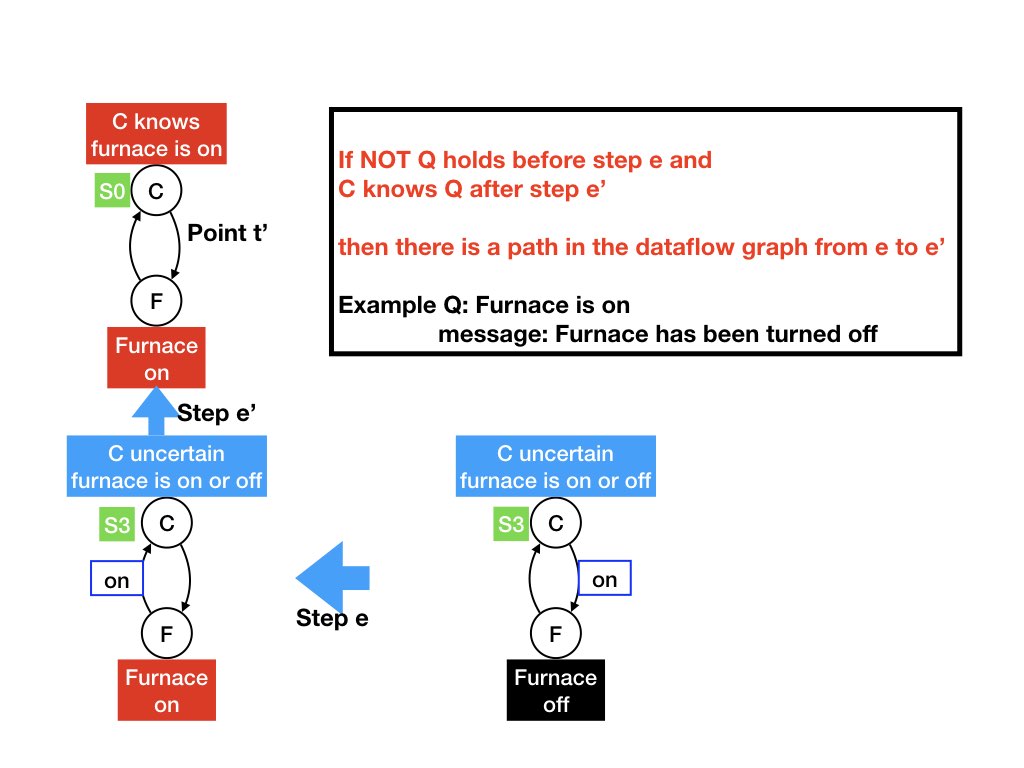
Let Q be a predicate and C an agent. If NOT Q holds before step e in a computation and C knows Q holds after a later step e' in the computation then there is a path from e to e' in the dataflow graph.

The theorem says that data must flow from a step in which predicate Q changes value to the step in which agent C knows that Q's value has changed.

Example

Q is the predicate: furnace is on. Let S1, S2, and S3 be the states shown in the diagrams at the bottom-right, bottom-left, on top-left respectively. Steps e and e' take the system from S1 to S2, and from S2 to S3, respectively.

NOT Q holds in S3 and C knows Q holds in S1. The theorem says that there exists a path in the dataflow graph from step e to step e'.

The figure below illustrates the theorem. Q is a predicate on the states of agent V. NOT Q holds before step 4 at V and Q holds after step 4.

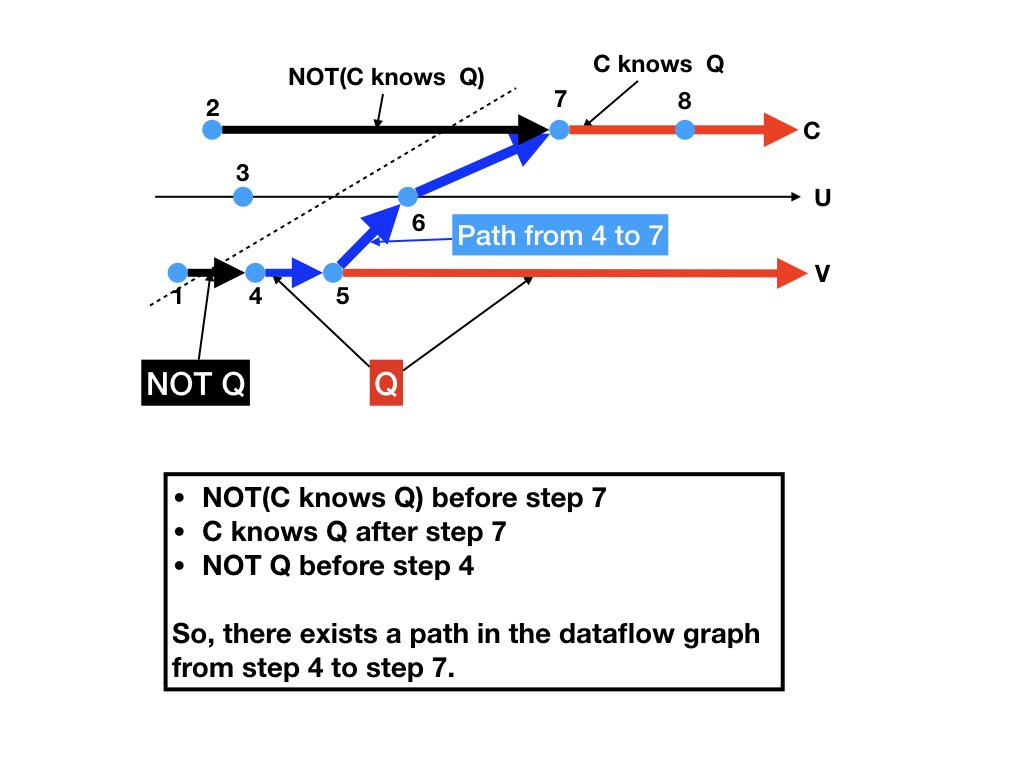
C knows Q after step 7. The theorem says there exists a path in the dataflow graph from step 4 to step 7.

Dual Theorem about Flow of Data to Lose Knowledge

Let Q be a predicate and C an agent. If C knows Q before a step e in a computation and NOT Q holds after a later step e' then there is a path from e to e' in the dataflow graph.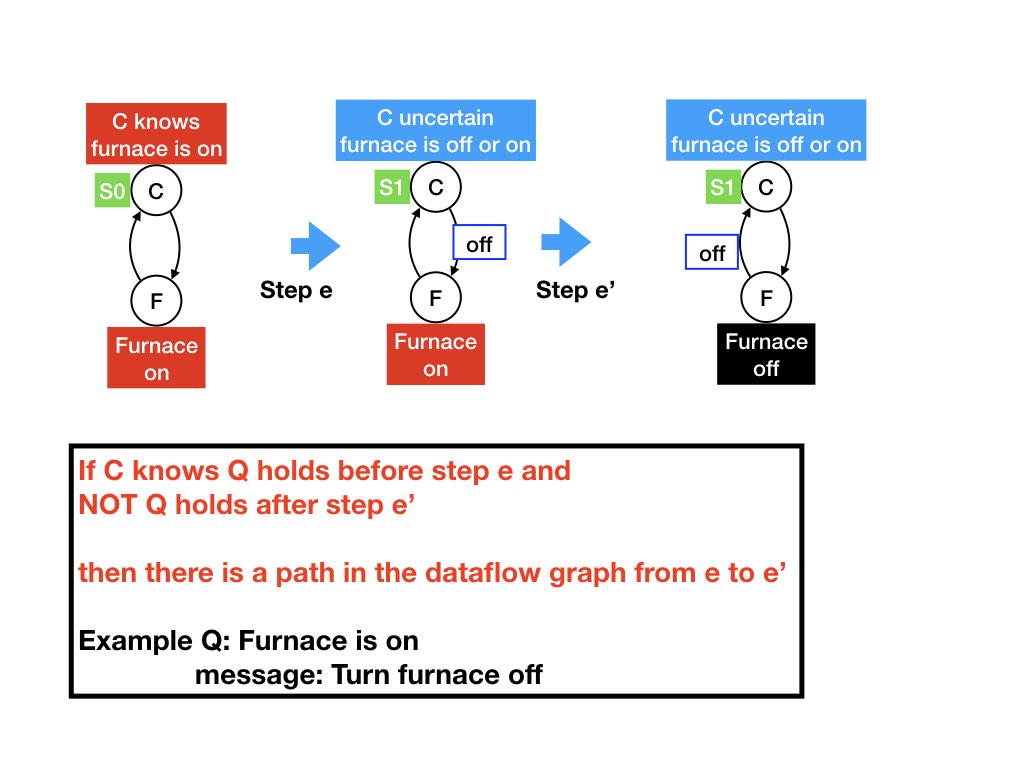

The theorem says that if an agent X knows that a predicate P holds for an agent Y then Y cannot make a state transition that falsifies P without "permission" from X -- data must flow from X to Y before Y can enter a state in which P is False.

Chains of Knowledge

Let \(x, y, z\) be agents of a system and \(P\) be a predicate on states of the system. Then the following are all predicates:

\(z\) knows \(P\)
\(y\) knows that \(z\) knows \(P\)
\(x\) knows that \(y\) knows that \(z\) knows \(P\)

The theorems given earlier apply to any predicate. For example, if \(x\) knows that \(y\) knows that \(z\) knows \(P\) at a point \(t\) in a trajectory, and \(\neg P\) holds at a later point \(t'\) then there must be path in the timeline diagram from point \(t\) on \(x\)'s timeline to point \(t'\) on \(z\)'s timeline.

The Role of Time

Loosely synchronized clocks

Next consider systems in which agent clocks are loosely synchronized. Each agent's clock drifts by at most \(\delta\) seconds from the true time. Suppose an agent \(x\) sends a message to an agent \(y\) where the message says that \(x\) will take an action -- say "turn the furnace on" -- at time \(T\) where \(T\) is determined by \(x\)'s clock, and that \(x\) will take a further action -- say "turn the furnace off" -- at a later time \(T'\). Assume that \(\delta\) is much smaller than \(T' - T\).

Agent \(y\) can gain knowledge about agent \(x\) without receiving messages for each action that \(x\) takes. When \(x\)'s clock reads \(T'\) then the true time lies in the interval \([T'-\delta, T'+\delta]\). When the true time is in this interval, agent \(y\)'s clock lies in the interval \([T'-2 \delta, T'+ 2\delta]\). So, when \(x\)'s clock reads \(T'\) then \(y\)'s clock reads a value in the interval \([T'-2\delta, T'+2\delta]\).

Agent \(y\) knows that \(x\) has taken the action -- "furnace is turned on" -- in the instant before \(T' - 2 \delta\). Agent \(y\) is unsure whether the action holds -- "is the the furnace on?" -- in the interval \([T' - 2\delta, T' + 2\delta]\). And \(y\) knows that the next action holds -- furnace is off -- at the instant after \(T'+2\delta\).

Bounded message delay

Consider a system in which message delays are positive and are at most \(\tau\). If \(x\) sends a message to \(y\) when \(x\)'s clock reads \(T\) then \(x\) knows at time \(T + \tau + \delta\) that \(y\) has received the message, and \(x\) gains this knowledge without \(y\) sending \(x\) a message.

Distributed cyber-physical systems with multiple sensors and actuators are systems with synchronized clocks (even if synchronization is imperfect) and with bounded delays. The discussion of what agents know show us why time plays a critical role in such systems.

Read Knowledge and Common Knowledge in a Distributed Environment and How Processes Learn.

Summary

Many people working on distributed systems use the phrase "an agent knows." This module gives a definition of the concept that is consistent with intuitive definitions of knowledge. The central idea in this module is the relationship between what agents know and consistent cuts of timelines. We presented several theorems about agent knowledge which are intuitive when applied to human agents. The proofs are straightforward and are all based on consistent cuts of timelines.

Review

1. Is the following true? Why?

   (\(z\) knows \(P\)) and (\(z\) knows \(Q\)) \(\equiv\) \(z\) knows (\(P \wedge Q\))

2. Is the following true? Why?

   (\(z\) knows \(P\)) or (\(z\) knows \(Q\)) \(\equiv\) \(z\) knows (\( P \vee Q\))

3. Suppose you and your friend communicate only using messages sent in channels, just as agents do in our model of distributed systems. When you know that your friend is wearing a cap does that mean that (a) your friend is wearing a cap, and (b) your friend can't take the cap off until the friend hears from you?